PROBABILITY & STATISTICS
Probability and statistics are related areas of mathematics which concern themselves with analyzing the relative frequency of events. Both subjects are important, relevant, and useful. But they are different, and understanding the distinction is crucial in properly interpreting the relevance of mathematical evidence.
Still, there are fundamental differences in the way they see the world:
| Probability | Statistics | |
|---|---|---|
| Goal: | Predicting the Future | Summarizing the Past |
| Branch of Mathematics: | Theoretical (pure math) | Application-driven (applied math) |
| Reasoning / Inference: | Deduction (Rules -> Data) | Induction (Data -> Rules) |
| Worldview: | Ideal | Real / Messy |
| Level of Confidence: | Certainty | Estimation |
| Researchers / Practitioners | Happy go-lucky | Tormented |
In summary, probability theory enables us to find the consequences of a given ideal world, while statistical theory enables us to measure the extent to which our world is ideal. This constant tension between theory and practice is why statisticians prove to be a tortured group of individuals compared with the happy-go-lucky probabilists.
This distinction will perhaps become clearer if we trace the thought process of a mathematician encountering their first gambling game:

Modern probability theory first emerged from gambling tables of France in mid 1600s. Blaise Pascal and Pierre de Fermat wondered whether the player or the house had the advantage in a particular betting game.
If a gambler were a probabilist, they would see the dice and think “Six-sided dice? Each side of the dice is presumably equally likely to land face up. Now assuming that each face comes up with probability 1/6, I can figure out what my chances are of winning.”
If instead a gambler were statistician, they would see the dice and think “How do I know that they are not loaded?” They’ll watch the game a while, and keep track of how often each number comes up. Then they can decide if my observations are consistent with the assumption of equal-probability faces. Once they have the probabilities figured out, they can call a probabilist to tell them how to bet.
In this course, we will use Statistics to go from Data to Probability-based models, as shown in the figure below:
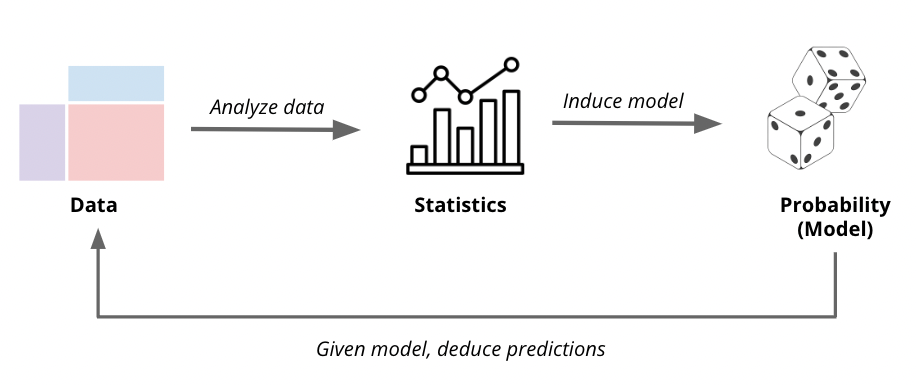
Having learned or estimated the model, we can then use Probability to make predictions about the future.