2-dimensional DP

2-d DP problems can be solved using a 2D array to store the results of subproblems. The array is typically indexed by two dimensions, representing the two parameters of the problem.

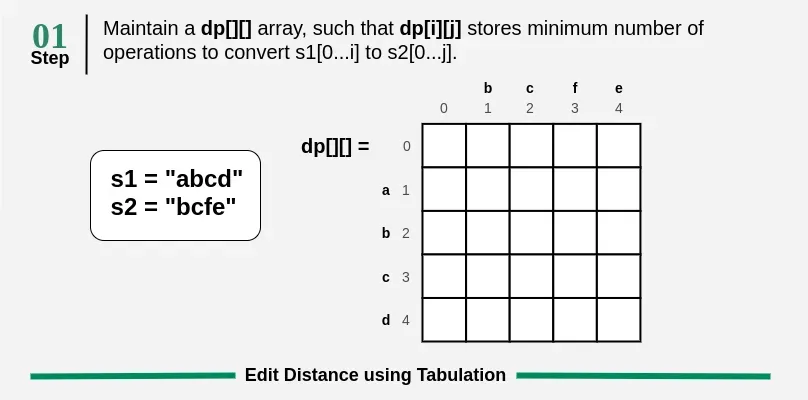
Edit Distance

Given two strings s1 and s2 and below operations that can be performed on s1. The task is to find the minimum number of edits (operations) to convert ’s1‘ into ’s2‘.

Insert: Insert any character before or after any index of s1 Remove: Remove a character of s1 Replace: Replace a character at any index of s1 with some other character.

public class EditDistance {
    public static int minDistance(String word1, String word2) {
        int m = word1.length();
        int n = word2.length();
        int[][] dp = new int[m + 1][n + 1];
        for (int i = 0; i <= m; i++) {
            for (int j = 0; j <= n; j++) {
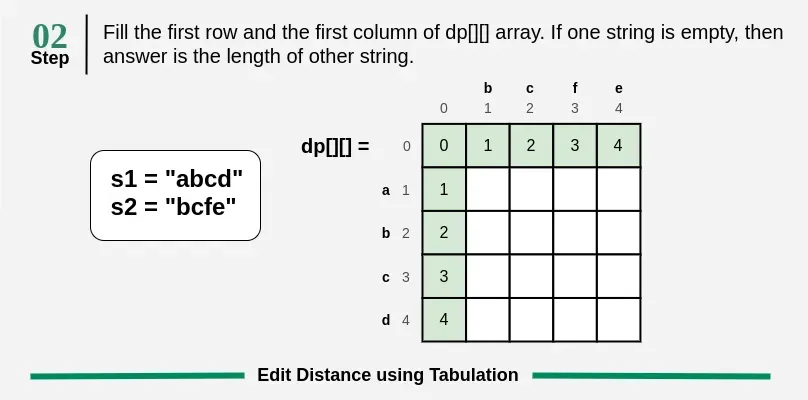
                if (i == 0) {
                    dp[i][j] = j;
                } else if (j == 0) {
                    dp[i][j] = i;
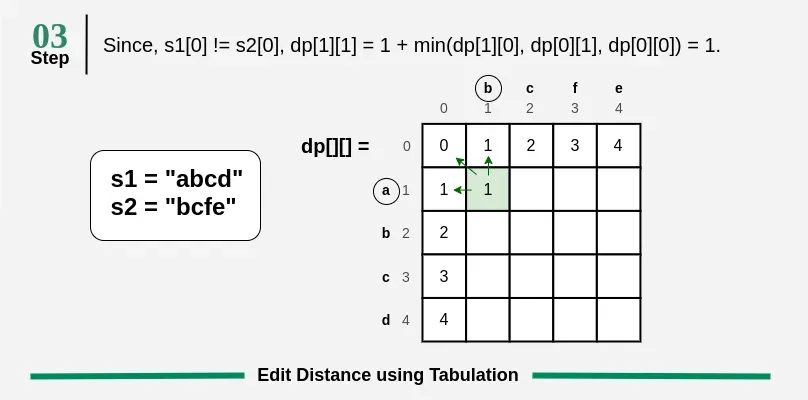
                } else if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = 1 + Math.min(dp[i - 1][j], Math.min(dp[i][j - 1], dp[i - 1][j - 1]));
                }
            }
        }
        return dp[m][n];
    }
}

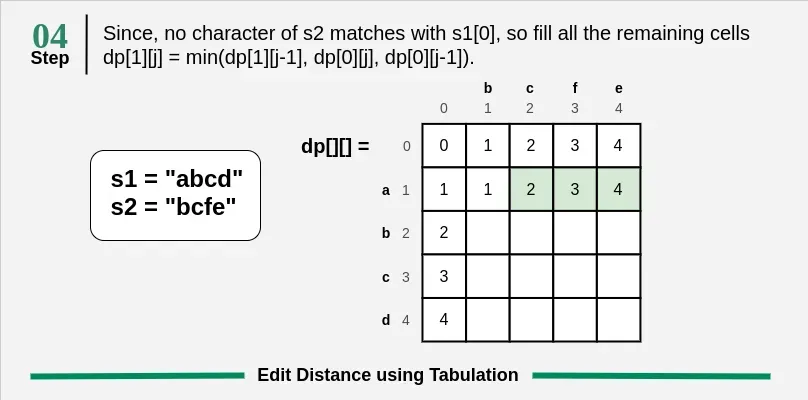
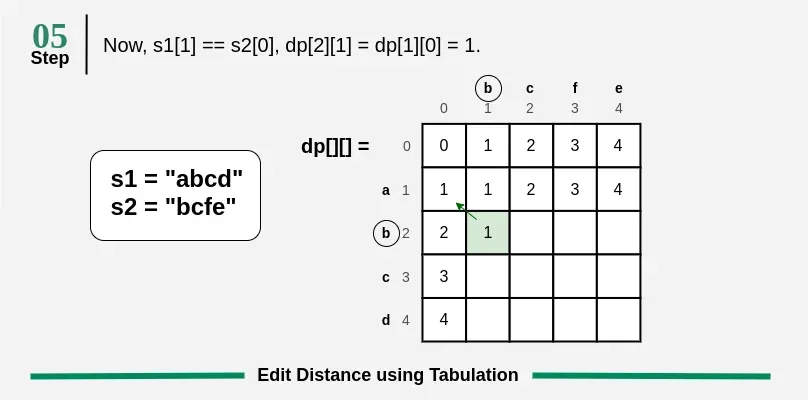
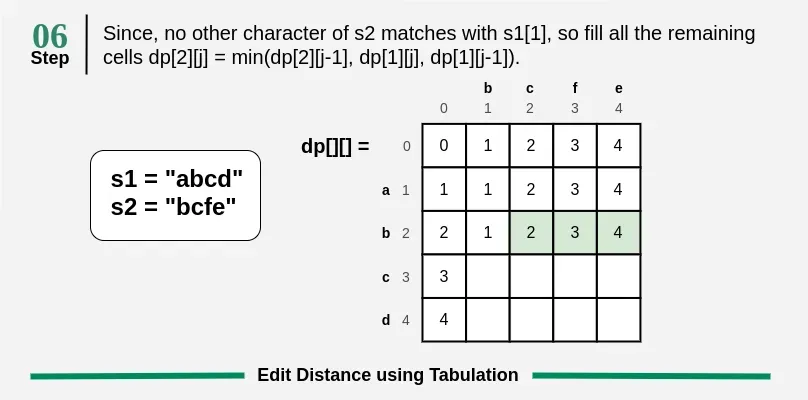
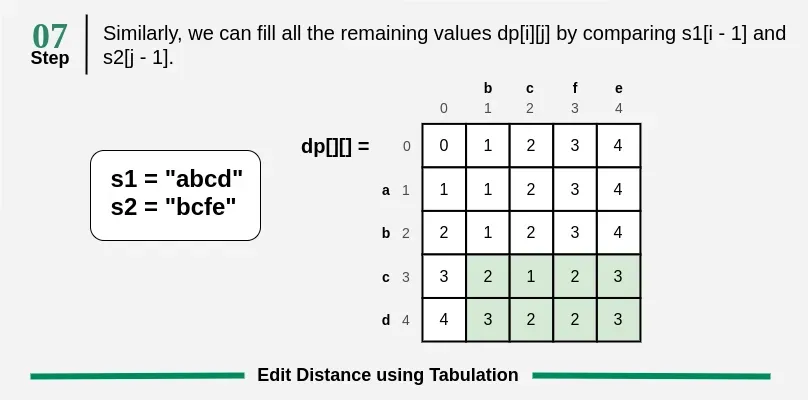
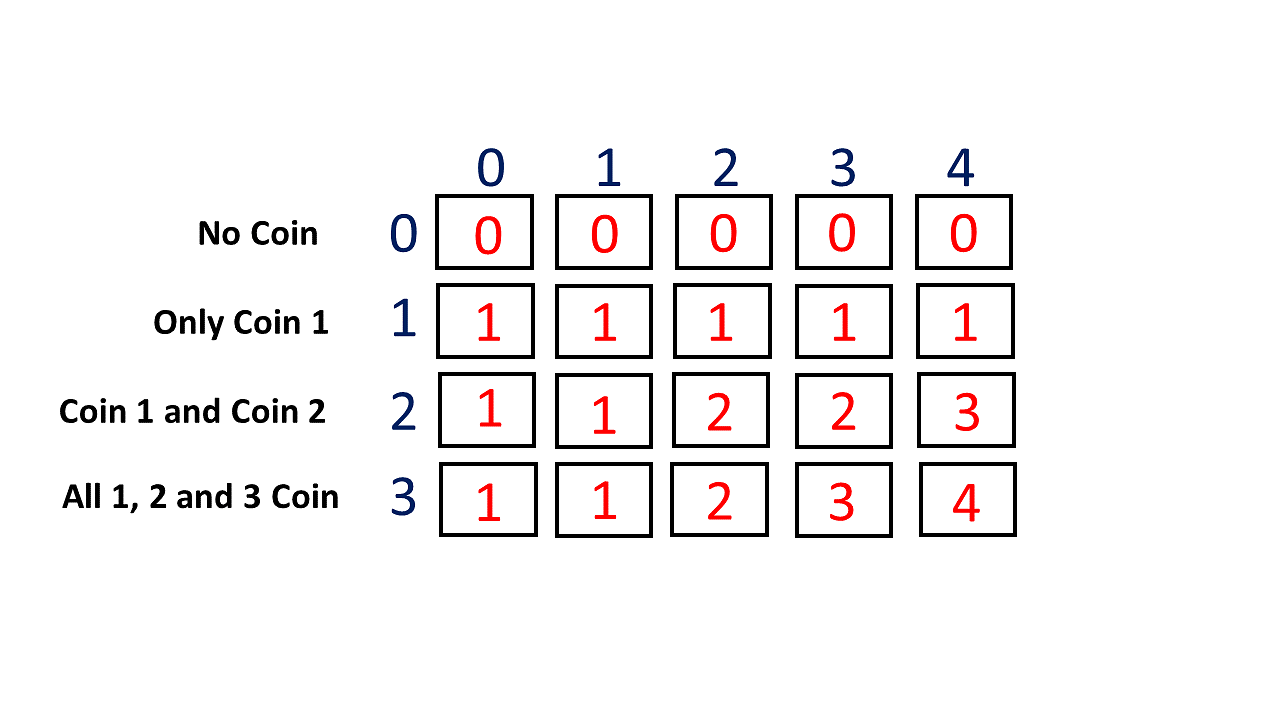
Coin Change Problem

The Coin Change Problem is a classic problem in dynamic programming. Given a set of coins of different denominations and a total amount, the goal is to find the minimum number of coins needed to make up that amount. If that amount cannot be made up by any combination of the coins, return -1.

public class CoinChange {
    public static int coinChange(int[] coins, int amount) {
        int[] dp = new int[amount + 1];
        Arrays.fill(dp, amount + 1);
        dp[0] = 0;
        for (int coin : coins) {
            for (int x = coin; x <= amount; x++) {
                dp[x] = Math.min(dp[x], dp[x - coin] + 1);
            }
        }
        return dp[amount] == amount + 1 ? -1 : dp[amount];
    }
}