Binary Search Tree
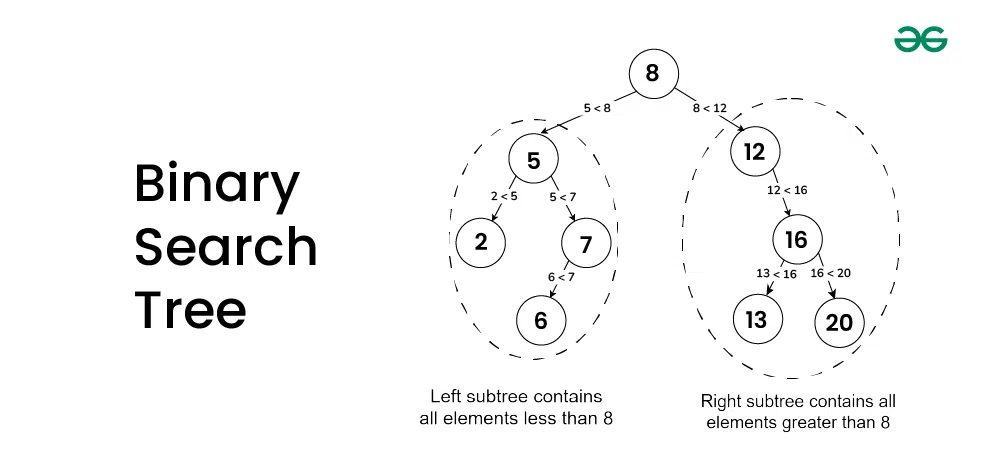
A binary search tree (BST) is a binary tree data structure that is used to store data in a sorted order.
The binary search tree must at all times satisfy the binary search tree property:
The left subtree of a node contains only nodes with values less than or equal to the node’s value.
The right subtree of a node contains only nodes with values greater than or equal to the node’s value.
Both the left and right subtrees must themselves be binary search trees>.
As a result of this property, the inorder traversal of a binary search tree will always return the nodes in sorted order.
Operations on Binary Search Trees
All operations on a binary search tree have a time complexity of O(h), where h is the height of the tree. h is equal to the number of levels in the tree.
For a balanced binary search tree, the height is O(log n), where n is the number of nodes in the tree.
For an unbalanced binary search tree, the height is O(n).
Search
Searching for a node in a binary search tree is very similar to searching for a value in a sorted array.
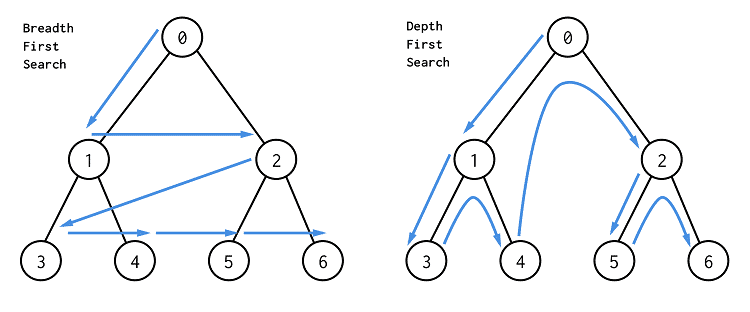
Depth First Search (DFS)
A traversal algorithm that explores as far as possible along each branch before backtracking.
Depth First Search can be implemented using the following steps:
If the tree is empty, return False.
If the current node is the target node, return True.
Recursively search the left subtree.
Recursively search the right subtree.
Breadth First Search (BFS)
A traversal algorithm that explores all the nodes at the present depth before moving on to the nodes at the next depth.
Breadth First Search can be implemented using the following steps:
If the tree is empty, return False.
Create a queue and add the root node to the queue.
While the queue is not empty, remove the first node from the queue.
If the current node is the target node, return True.
Add the left child of the current node to the queue if it exists.
Add the right child of the current node to the queue if it exists.
Insertion

Adding a new node to the tree follows the following steps:
If the tree is empty, create a new node and set it as the root of the tree.
If the tree is not empty
Compare the value of the new node with the value of the current node.
If the value of the new node is less than the value of the current node, move to the left subtree.
If the value of the new node is greater than the value of the current node, move to the right subtree.
Repeat steps 2.1 to 2.3 until you reach a leaf node.
- Insert the new node as the left child if the value of the new node is less than the value of the leaf node, or as the right child if the value of the new node is greater than the value of the leaf node.
Deletion
Deletion of a node in a binary search tree involves the following steps:
If the tree is empty, return the tree.
If the value of the node to be deleted is less than the value of the current node, move to the left subtree.
If the value of the node to be deleted is greater than the value of the current node, move to the right subtree.
If the value of the node to be deleted is equal to the value of the current node, delete the node.
If the node has no children, simply delete the node.
If the node has one child, replace the node with its child.
If the node has two children, find the inorder successor of the node, replace the node with the inorder successor, and delete the inorder successor.
The inorder successor is the smallest node in the right subtree of the node to be deleted.
Case 1: Node to be deleted has no children 
Case 2: Node to be deleted has one child 
Case 3: Node to be deleted has two children 
Update
Updating a node in a binary search tree involves deleting the node and inserting a new node with the updated value.
The time complexity of inserting a node in a binary search tree is O(h), where h is the height of the tree.
The time complexity of deleting a node in a binary search tree is also O(h), where h is the height of the tree.
Therefore, the time complexity of updating a node in a binary search tree is O(h).