Collision Avoidance
There are mainly two methods to handle collision:
Open Addressing
In open addressing, all elements are stored in the hash table itself. When a new element is inserted, the hash function is computed and if the slot is already occupied, then the next slot is checked. This process continues until an empty slot is found.
Open Addressing has the following techniques:
Linear Probing
Search for an empty slot sequentially. The next slot is checked if the current slot is occupied. This process continues until an empty slot is found.
Formally, the probing sequence is given by:
\[ h(k, i) = (h'(k) + i) \mod m \]
where:
- \(h(k, i)\) is the probing sequence
- \(h'(k)\) is the hash function for key \(k\) such that \(0 \leq h'(k) < m\)
- \(m\) is the size of the hash table
- \(i\) is the probe number
When insertions are done in a linear sequence, searching for an element is also done in a linear sequence.
To check if an element is present in the hash table, the same probing sequence is used to find the slot where the element should be located. If the element is found at that slot, then it is present in the hash table. If a different element is found at that slot, then the search continues by checking the next slot in the probing sequence.
Quadratic Probing
Search for an empty slot using a quadratic function
Formally, the probing sequence is given by:
\[ h(k, i) = (h'(k) + c_1 \cdot i + c_2 \cdot i^2) \mod m \]
where:
- \(h(k, i)\) is the probing sequence
- \(h'(k)\) is the hash function for key \(k\) such that \(0 \leq h'(k) < m\)
- \(m\) is the size of the hash table
- \(i\) is the probe number
- \(c_1\) and \(c_2\) are constants
The quadratic probing technique uses a quadratic function to compute the next slot to check when resolving collisions. This technique reduces the clustering effect that can occur with linear probing and spreads out the elements more evenly in the hash table.
Double Hashing
Use a second hash function to find the next slot. If the slot is already occupied, a second hash function is used to compute the next slot to check. This process continues until an empty slot is found.
Formally, the probing sequence is given by:
\[ h(k, i) = (h_1(k) + i \cdot h_2(k)) \mod m \]
where:
- \(h(k, i)\) is the probing sequence
- \(h_1(k)\) is the primary hash function for key \(k\) such that \(0 \leq h_1(k) < m\)
- \(h_2(k)\) is the secondary hash function for key \(k\) such that \(0 < h_2(k) < m\)
- \(m\) is the size of the hash table
Double hashing uses two hash functions to compute the next slot to check when resolving collisions. The secondary hash function is used to compute the step size for probing, which can help reduce clustering and distribute the elements more evenly in the hash table.
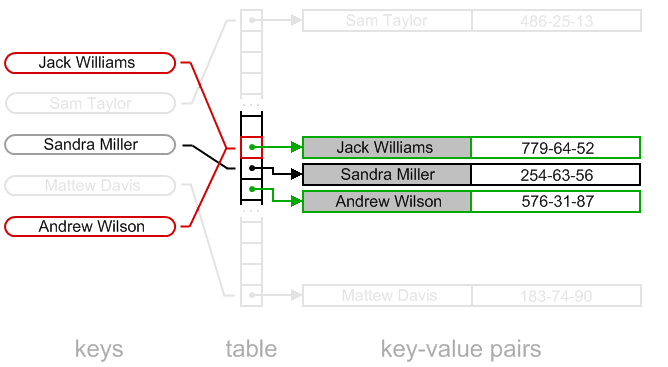
Separate Chaining
In separate chaining, each slot of the hash table is a linked list. When a new element is inserted, the hash function is computed and the element is inserted at the head of the linked list at that slot. This allows multiple elements to be stored at the same slot.

Separate chaining has the following characteristics:
- Each slot in the hash table is a linked list
- When a new element is inserted, it is added to the head of the linked list at that slot
- When searching for an element, the hash function is computed to find the slot, and then the linked list at that slot is searched for the element
Separate chaining is a simple and effective collision resolution technique that allows multiple elements to be stored at the same slot in the hash table. It is commonly used in hash table implementations and provides good performance for a wide range of applications.