HASHING

Hashing refers to the process of mapping data values (refered to as keys) to a specific location in the data structure that enables reading, writing, and searching operations to be performed far more efficiently than possible with other data structures.

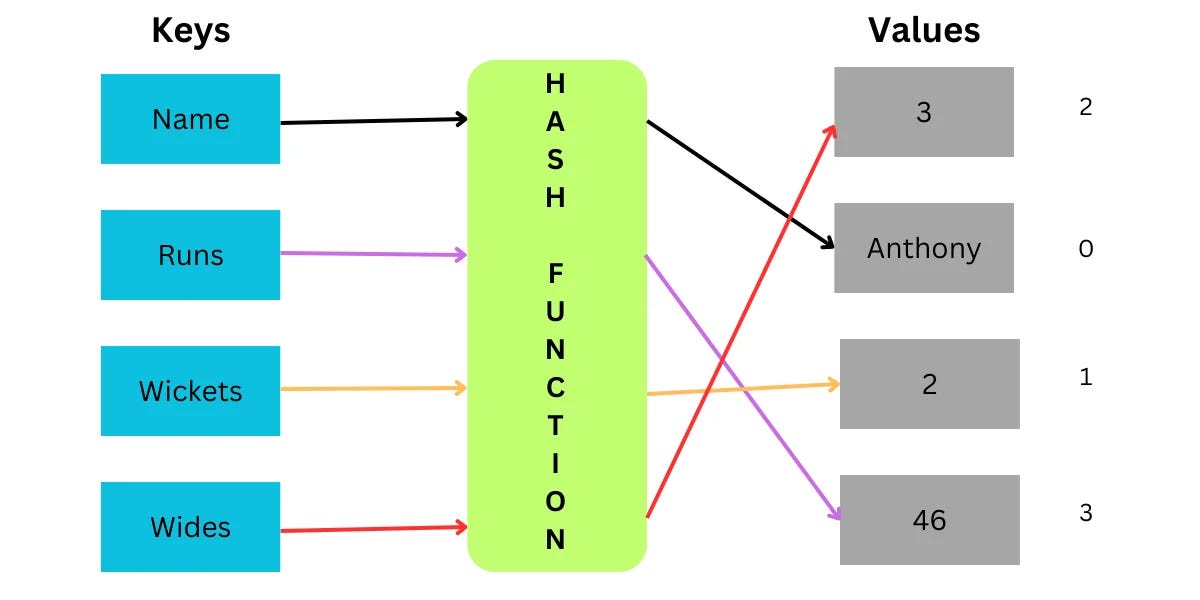
The transformation of a key to the corresponding value is done using a Hash Function and the value obtained from the hash function is called Hash Code or simply hashes.

Hashing is used in various applications such as databases, caches, and programming languages to optimize search and retrieval operations.

Example

Suppose we want to store string values in a data structure, say array, of size 7. We then need to map the string values to a specific index in the internal array. We can use a hash function to map the strings to a specific index in the data structure.

One simple hash function is to consider the position of each character in the string values in the English alphabet and sum them up. For example, the hash value of “abc” would be 1 + 2 + 3 = 6. The hash value of “xyz” would be 24 + 25 + 26 = 75. We can then use the modulo operator % to map the hash value to an index in the array.

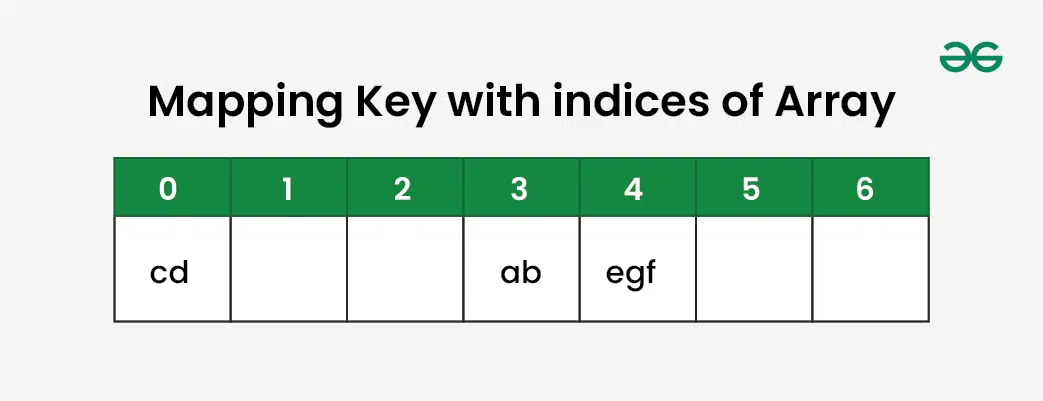
Other possible simple hash functions could have been to consider only the first or last character of the string, instead of summing all the characters. Another option could be to sum the ASCII values of the characters in the string or to use the length of the string as the hash value.

Collisions

If we consider the above example, the hash function we used is the sum of the letters, but if we examined the hash function closely then the problem can be easily visualized that for different strings same hash value is being generated by the hash function.

For example: {“ab”, “ba”} both have the same hash value, and string {“cd”,”be”} also generate the same hash value, etc. This is known as collision and it creates problem in searching, insertion, deletion, and updating of value.

Collision in Hashing occurs when two different keys map to the same hash value. Hash collisions can be intentionally created for many hash algorithms. The probability of a hash collision depends on the size of the algorithm, the distribution of hash values and the efficiency of Hash function.

The hashing process generates a small number for a big key, so there is a possibility that two keys could produce the same value. The situation where the newly inserted key maps to an already occupied, and it must be handled using some collision handling technology.

Load Factor

The load factor of a hash table is the ratio of the number of elements stored in the hash table to the size of the hash table. It is used to measure how full the hash table is and can affect the performance of the hash table.

The load factor is calculated as:

\[ \text{Load Factor} = \frac{\text{Number of Elements}}{\text{Size of Hash Table}} \]

A high load factor means that the hash table is full and may have more collisions, which can slow down operations. A low load factor means that the hash table is not full and may have more empty slots, which can waste memory.

The load factor is used to determine when to resize the hash table. When the load factor exceeds a certain threshold, the hash table is resized to a larger size to reduce the number of collisions and improve performance.

Hash Set vs. Hash Map

Hashing is used to implement two common data structures: hash sets and hash maps (also known as dictionaries).

A hash set is a data structure that stores a collection of unique elements, similar to a set in mathematics. A hash set uses a hash table to store the elements and provides fast search, insert, and delete operations.

A hash map is a data structure that stores key-value pairs, similar to a dictionary in Python. A hash map uses a hash table to store the key-value pairs and provides fast search, insert, and delete operations based on the keys.

Analysis

The time complexity of hash table operations depends on the efficiency of the hash function and the collision resolution technique. In general, hash table operations have an average-case time complexity of O(1) for search, insert, and delete operations.

The space complexity of a hash table is O(n), where n is the number of key-value pairs stored in the table. The space complexity can vary based on the load factor and the collision resolution technique used.