Heaps

A heap is a binary tree with the following properties:

  1. It is a complete binary tree:

    All levels of the tree are fully filled except possibly for the last level, which is filled from left to right.

  2. It satisfies one of the heap property, depending on the type of heap:

    • In a Max-heap, the value of each node is greater than or equal to (\(\geq\)) the values of its children.

    • In a Min-heap, the value of each node is less than or equal to (\(\leq\)) the values of its children.


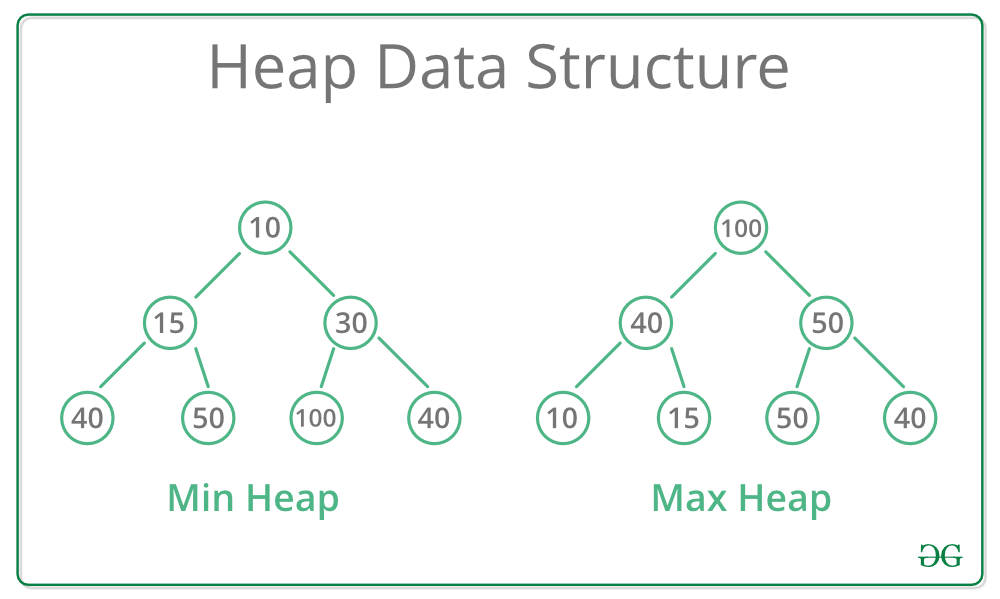
The heap property guarantees that the largest (in a max-heap) or smallest (in a min-heap) value is always at the root, and the tree maintains a specific order based on the type of heap.


Array-based Implementation

Heaps can be implemented using arrays or linked lists. The following is an implementation of a max-heap using an array:



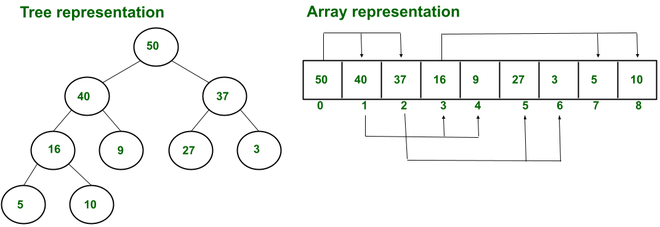
There are several ways to implement a heap, including using arrays, linked lists, or binary trees.

Heaps are commonly implemented using arrays, where the root element is stored at index 0, and the children of the node at index \(i\) are stored at indices \(2i + 1\) and \(2i + 2\).


Node Position in Array
Root 0
Left Child of node at index \(i\) \(2i + 1\)
Right Child of node at index \(i\) \(2i + 2\)
Parent of node at index \(i\) \[\lfloor \frac{i-1}{2} \rfloor\]


This representation allows for efficient access to the parent and children of a node.

Operations

A heap supports the following operations:

  1. Insert: Insert an element into the heap, maintaining the heap property and the complete binary tree property.

  2. Extract / Delete: Remove and return the root element of the heap, maintaining the heap property and the complete binary tree property.

  3. Heap Sort: Sort an array using a heap.



Insert

Inserting an element into a heap involves the following steps:

  1. Add the element to the end of the heap, maintaining the complete binary tree property i.e. fill from left to right at the last level.
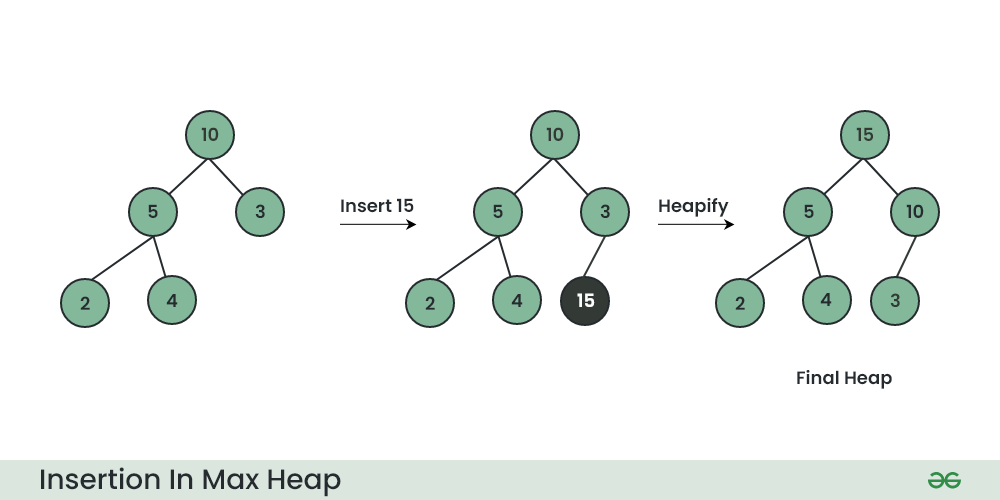
Step 1: Add the element to the end of the heap. Step 2: Heapify


  1. Bubble Up (Heapify): Restore the heap property by swapping the element with its parent until the heap property is satisfied.
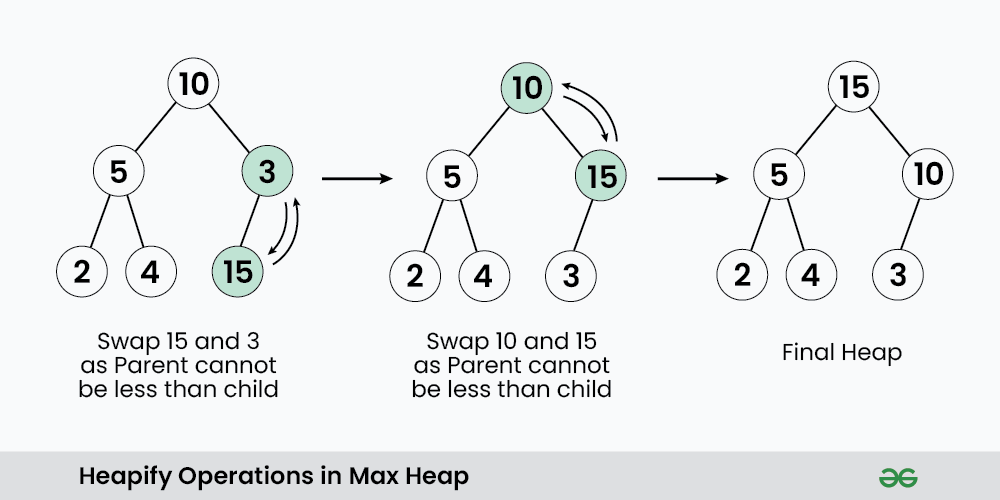
Step 2: Heapify (broken down into substeps)

Bubble up is an example of a heapify operation that moves an element up the heap until the heap property is satisfied.

For a max-heap, the element is moved up the heap until it is greater than or equal to its parent or until it reaches the root.

For a min-heap, the element is moved up the heap until it is less than or equal to its parent or until it reaches the root.

The time complexity of inserting an element into a heap is \(O(\log n)\), where \(n\) is the number of elements in the heap. Step 1 takes \(O(1)\) time, and step 2 (heapify) takes \(O(\log n)\) time to go from the leaf to the root.



Read / Peek

Reading or peeking at the root element of a heap involves returning the value of the root element without removing it from the heap.

Extract / Delete

Deleting from a heap (also known as extracting) always involves removing the root element from the heap.

Extracting the maximum element from a max-heap or the minimum element from a min-heap involves the following steps:


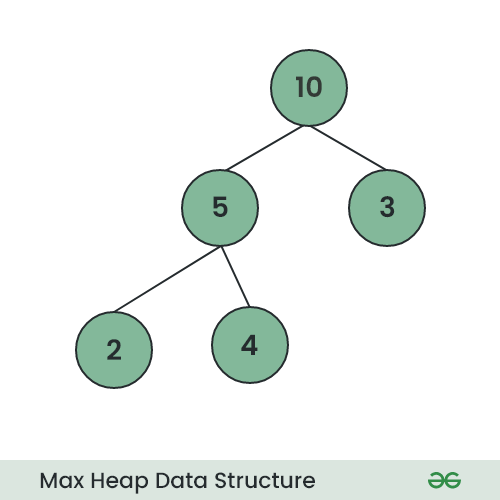
  1. Replace the root element with the last element in the heap (rigthmost element in the last level).

  2. Remove the last element from the heap.

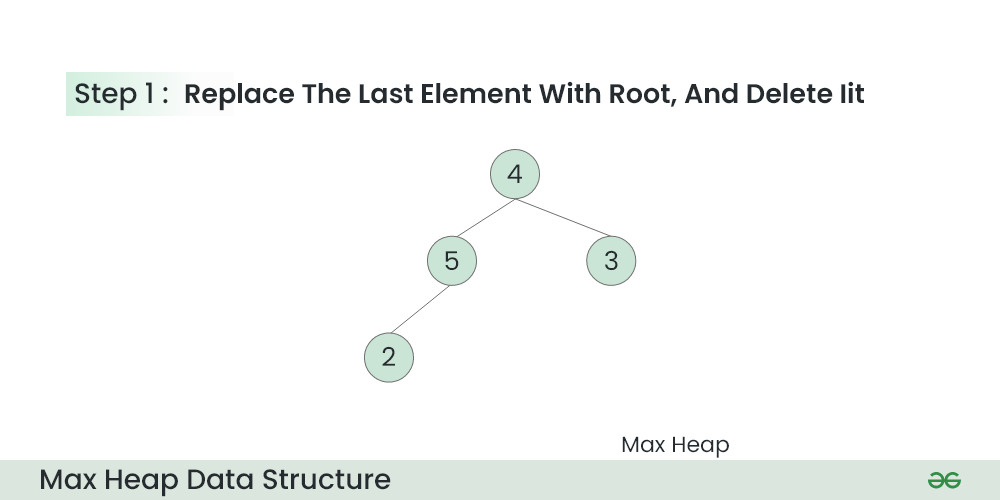
Step 1: Replace the root element with the last element. Step 2: Remove the last node


  1. Bubble Down: Restore the heap property by moving the new root element down the heap until the heap property is satisfied.


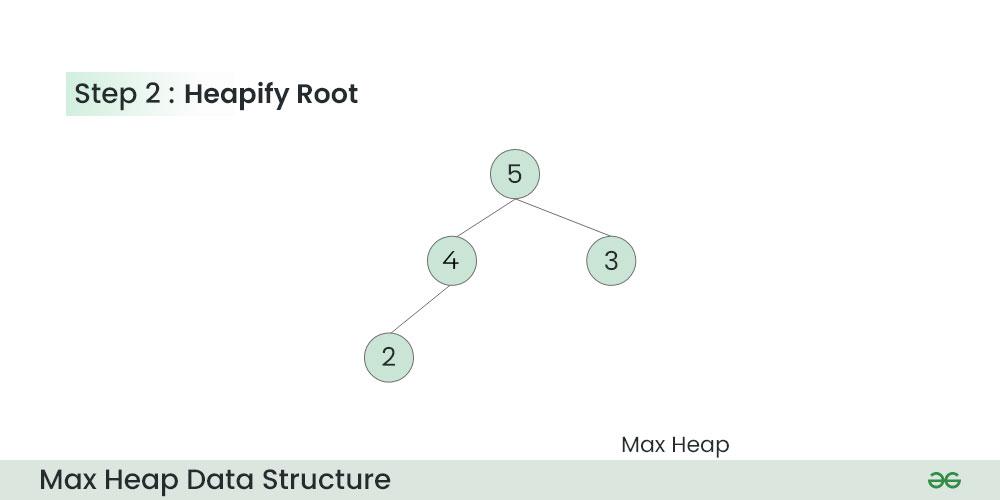
Step 3: Heapify (broken down into substeps)


Heapify

Heapify is an operation that restores the heap property in a heap. It involves moving an element up (bubble up) or down the heap (bubble down) to satisfy the heap property.

Generally, heapify is used after an insert or extract operation to maintain the heap property.


Heapify Type 1: Bubble Up

Bubble up is needed after inserting an element into a heap to maintain the heap property. It involves moving the element up the heap until the heap property is satisfied.

Regardless of the type of heap (max-heap or min-heap), bubble up is fairly simple and consists of the following steps:

  1. Compare the element with its parent.
  2. If the element is greater than (in a max-heap) or less than (in a min-heap) its parent, swap the element with its parent.
  3. Repeat steps 1 and 2 until the heap property is satisfied or until the element reaches the root.


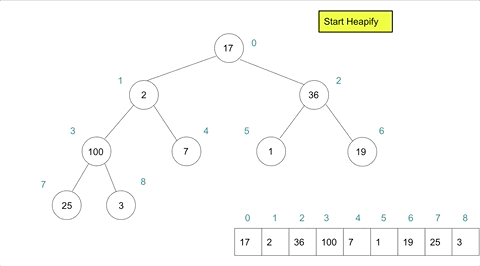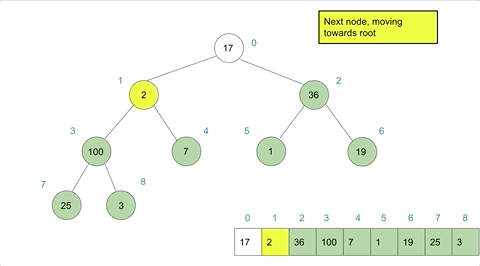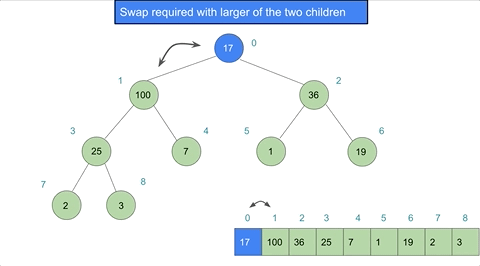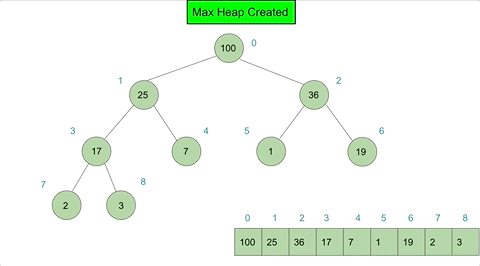
Heapify Type 2: Bubble Down

Bubble down is needed after extracting an element from a heap to maintain the heap property. It involves moving an element down the heap until the heap property is satisfied.

Bubble down is a little more complex than bubble up and consists of the following steps:

For a max-heap:

  1. Set current position to 0 (the root).
  2. Compare the element at current position with its children.
  3. Swap the element with the larger of its children.
  4. The new current position is the index of the child that the element was swapped with.
  5. Repeat steps 1 and 2 until

    • the heap property is satisfied:

      OR

    • until the element reaches the last level.

For a min-heap:

  1. Set current position to 0 (the root).
  2. Compare the element at current position with its children.
  3. Swap the element with the smaller of its children.
  4. The new current position is the index of the child that the element was swapped with.
  5. Repeat steps 1 and 2 until

    • the heap property is satisfied:

      OR

    • until the element reaches the last level.

Applications

Heaps are used in various applications, including:

Priority Queues

A priority queue is an abstract data type, often implemented using a heap, that allows elements to be inserted and extracted based on their priority.

The element with the highest priority is at the root of the heap (max-heap) or the element with the lowest priority is at the root of the heap (min-heap).

Priority queues are commonly used in algorithms and applications where elements need to be processed based on their priority, such as task scheduling, Dijkstra’s algorithm, Prim’s algorithm, Huffman coding, and more.

Note that the terms “max-priority queue” and “min-priority queue” are used interchangeably with “max-heap” and “min-heap,” respectively, when implementing priority queues using heaps.


Please note that priority queue are distinct from queues or stacks, which are first-in-first-out (FIFO) and last-in-first-out (LIFO) data structures, respectively.

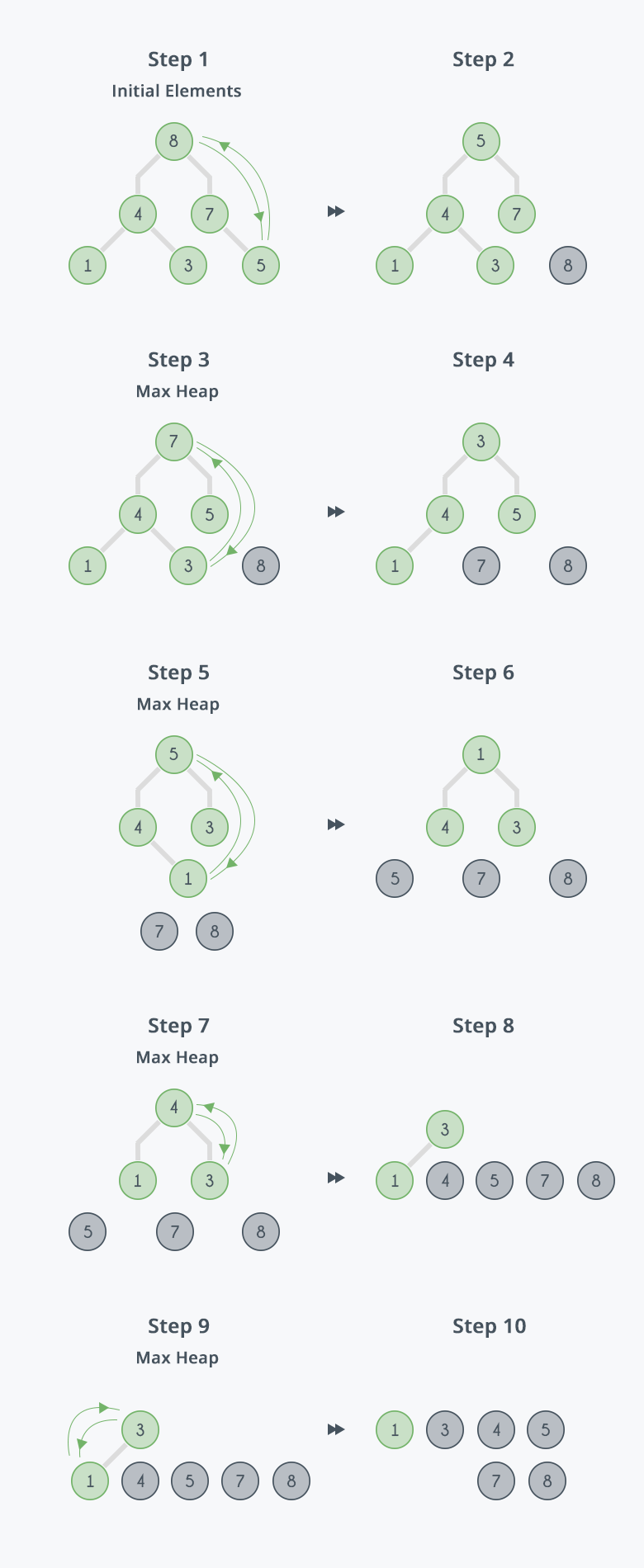
Heap Sort

Heap sort is a sorting algorithm that uses a heap to sort an array. It involves converting the array into a heap using the heapify operation and then extracting the root element of the heap until the heap is empty.

Heap sort involves the following steps:

  1. Build Heap: Convert the array into a heap using the heapify operation.

  2. Extract Max/Min: Repeatedly extract the maximum (in a max-heap) or minimum (in a min-heap) element from the heap until the heap is empty.

  3. Sort: The extracted elements form a sorted array.



Heap sort has a time complexity of \(O(\text{n log n})\) and is an in-place sorting algorithm with a space complexity of \(O(1)\).