Bellman-Ford Algorithm
Dijkstra’s algorithm cannot handle negative weights because it assumes that once a node is reached with the shortest possible distance, there’s no need to revisit or update that distance later. This assumption holds true for graphs with only non-negative edge weights but fails when negative weights are present.
To handle graphs with negative weights, the Bellman-Ford algorithm is typically used. The Bellman-Ford algorithm can also be used for graphs with positive edges (both directed and undirected), like we can with Dijkstra’s algorithm, but Dijkstra’s algorithm is preferred in such cases because it is faster.
Unlike Dijkstra’s algorithm, Bellman-Ford doesn’t rely on the greedy process of visiting each node in order of the current shortest known distance. Instead, Bellman-Ford performs multiple passes to “relax” each edge, ensuring that it correctly updates the shortest path distances even in the presence of negative weights. It also detects negative cycles, making it more robust for such cases.
Key Insight of Bellman-Ford Algorithm
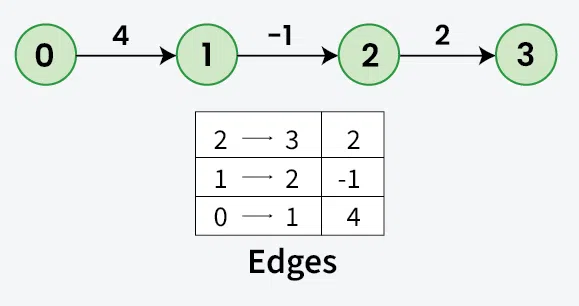
Worst case scenario the shortest path between two vertices in a graph with V vertices and E edges is V-1 edges. So, we need to relax all edges V-1 times to find the shortest path between two vertices.
Pseudocode
The Bellman-Ford algorithm is best suited to find the shortest paths in a directed graph, with one or more negative edge weights, from the source vertex to all other vertices.
It does so by repeatedly checking all the edges in the graph for shorter paths, as many times as there are vertices in the graph (minus 1).
Bellman-Ford algorithm is a single-source shortest path algorithm that can handle graphs with negative edge weights.
The steps of the Bellman-Ford algorithm are as follows:
Set initial distance to zero for the source vertex, and set initial distances to infinity for all other vertices.
‘Relax’ all edges \(V-1\) times, where V is the number of vertices in the graph.
For each edge, check if a shorter distance can be calculated, and update the distance if the calculated distance is shorter.
Relax an edge (u, v) means to update the distance to vertex v if the distance to vertex u plus the weight of edge (u, v) is less than the current distance to vertex v.
Check all edges (step 2) \(V−1\) times. This is as many times as there are vertices (\(V\)), minus one.
Optional: Check for negative cycles. This will be explained in better detail later. Check for negative weight cycles by relaxing all edges one more time. If any distance is updated in this step, then the graph contains a negative weight cycle.
Negative Cycles
Using the Bellman-Ford algorithm on a graph with negative cycles will not produce a result of shortest paths because in a negative cycle we can always go one more round and get a shorter path.
A negative cycle is a path we can follow in circles, where the sum of the edge weights is negative.
Luckily, the Bellman-Ford algorithm can be implemented to safely detect and report the presence of negative cycles.
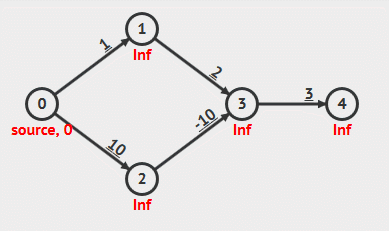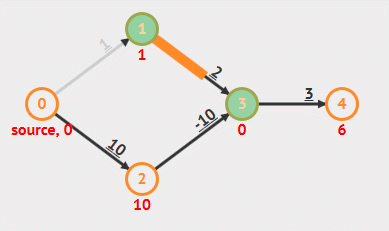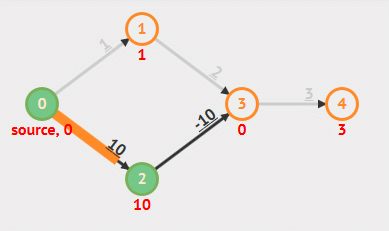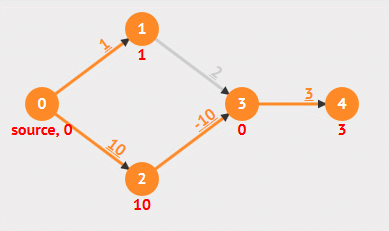
The time complexity of Bellman-Ford algorithm is O(V*E), where V is the number of vertices and E is the number of edges in the graph.
Example
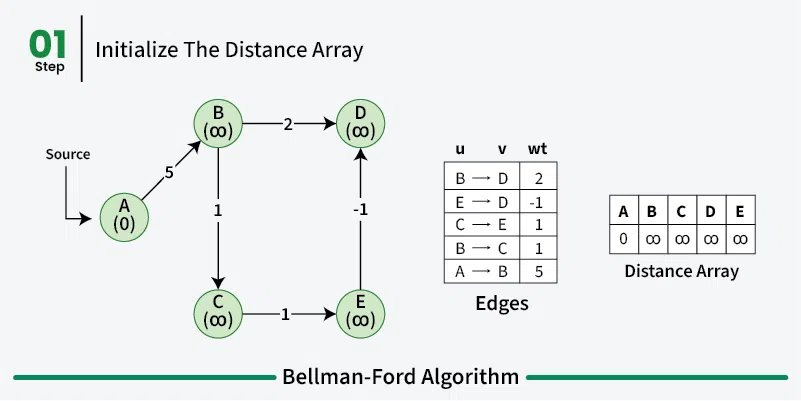

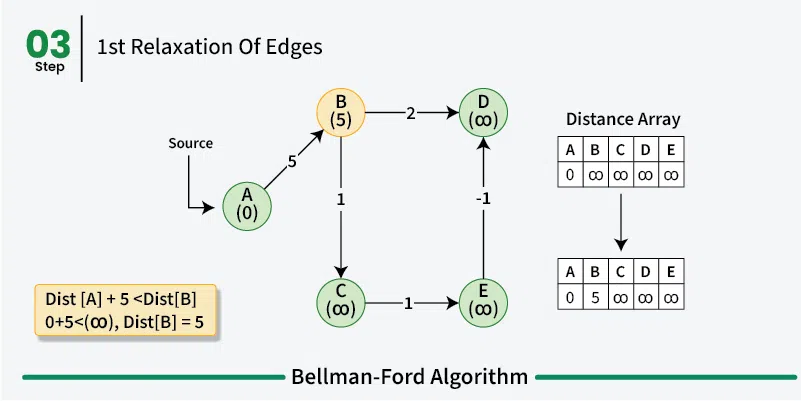
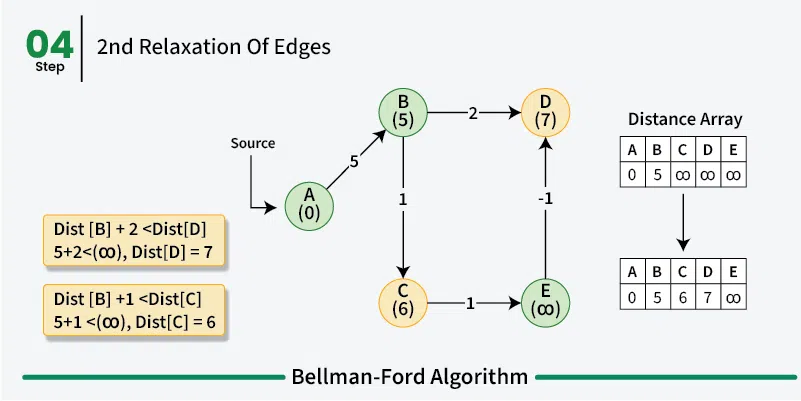
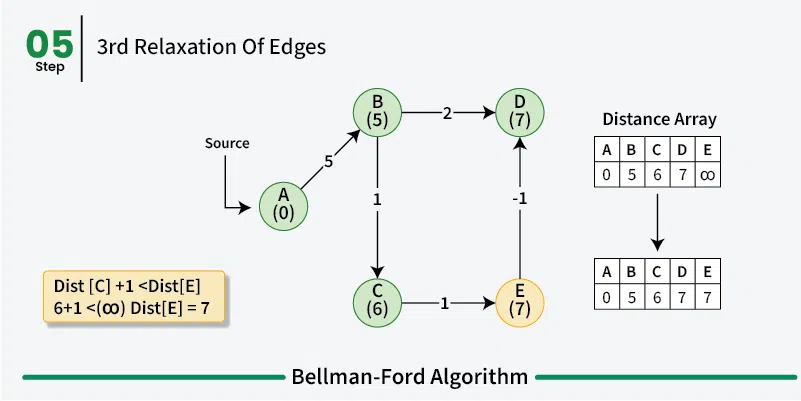
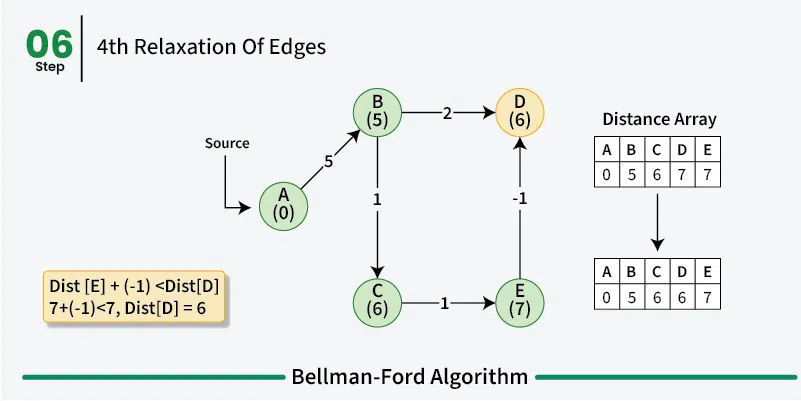
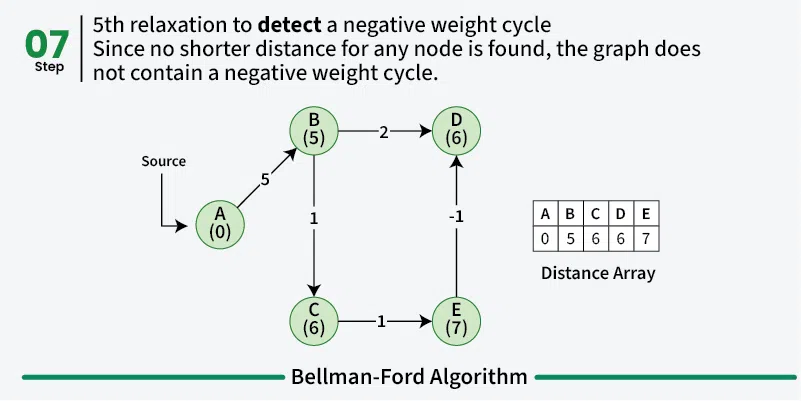
Analysis
The time complexity of Bellman-Ford algorithm is O(V*E), where V is the number of vertices and E is the number of edges in the graph.
The space complexity of Bellman-Ford algorithm is O(V), where V is the number of vertices in the graph.