BFS-based: Kahn’s Algorithm
Kahn’s algorithm is used to find a topological ordering of the vertices in a DAG. It is based on the concept of in-degree, which is the number of incoming edges to a vertex.
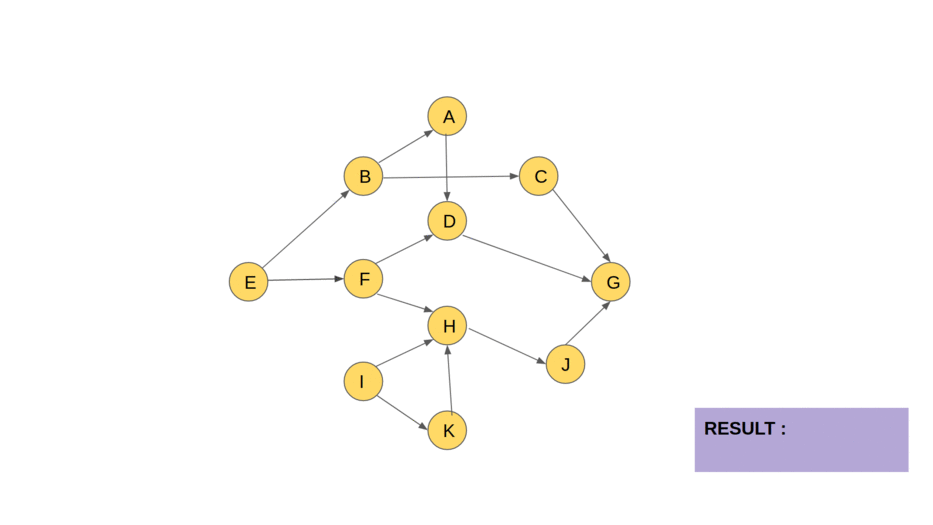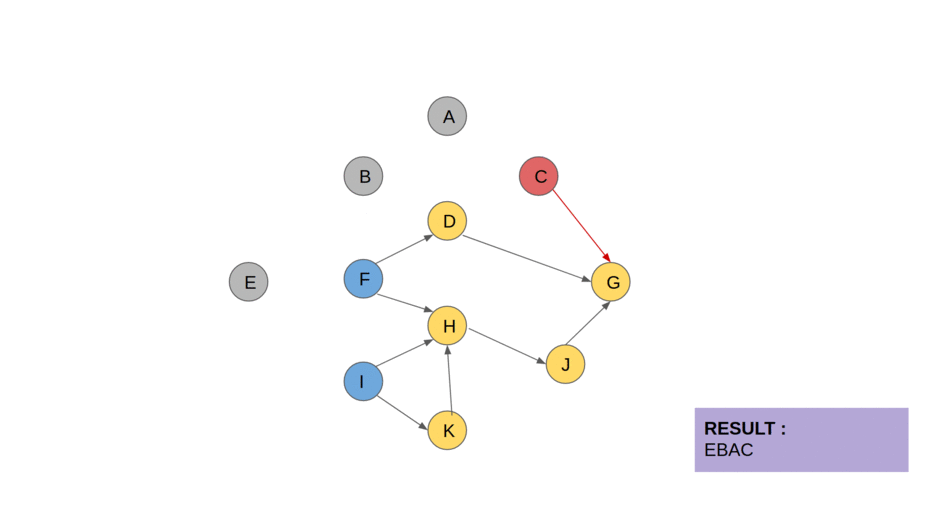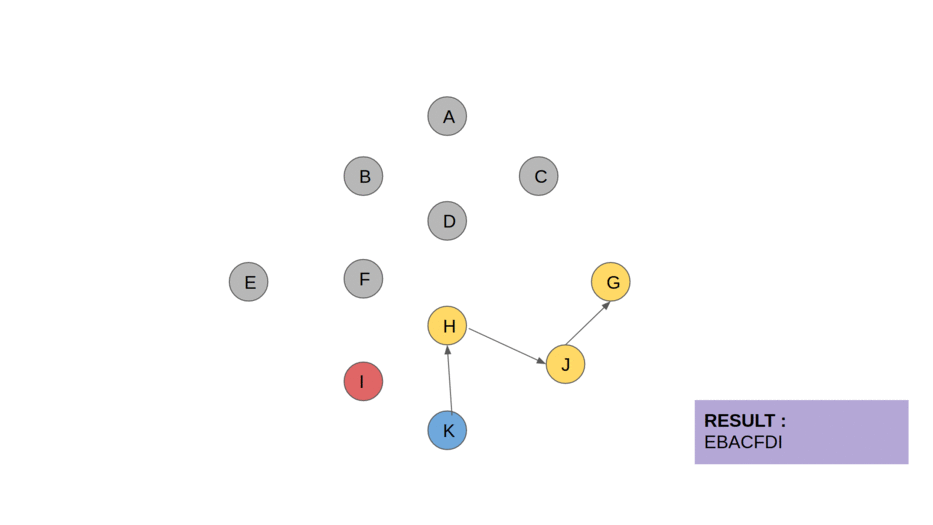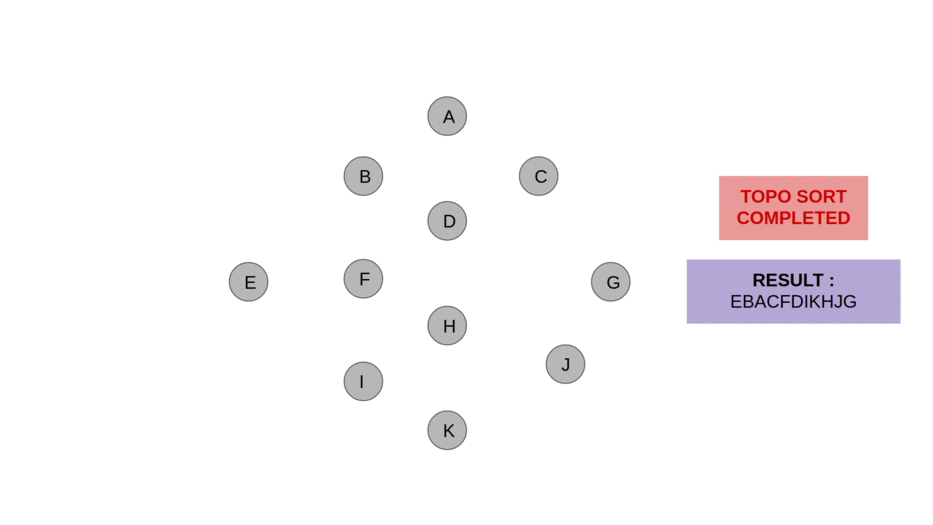
Kahn’s algorithm is a method used to compute the topological order of vertices in a directed acyclic graph (DAG). It relies on the concept of In-degree, which is the count of incoming edges for each vertex.
The algorithm identifies vertices with no incoming edges (in-degree 0) as starting points for the ordering. These vertices can be processed first because they have no dependencies. To keep track of in-degrees, the algorithm uses an array called InDegree. It also uses a list called Sorted to store the topological order as it is constructed and a Queue to manage vertices with in-degree 0.
Next, all vertices with an in-degree of 0 are added to the queue, as they can be processed immediately. The algorithm then enters a loop, where it repeatedly removes a vertex from the queue, adds it to the Sorted list, and processes its neighbors. For each neighbor, the algorithm reduces its in-degree by 1 to reflect that one of its dependencies has been processed. If a neighbor’s in-degree becomes 0, it is added to the Queue, making it ready for processing in subsequent iterations.
This process continues until the queue is empty. If all vertices have been added to the Sorted list by the end, the algorithm returns the list as the topological order. However, if some vertices remain unprocessed (i.e., the Sorted list does not contain all vertices), it indicates the presence of a cycle in the graph, which makes a topological order impossible. This systematic approach ensures that vertices are processed only after all their dependencies have been handled, making it a reliable method for topological sorting.
Pseudocode
The pseudocode for Kahn’s algorithm is as follows:
Function: \(topologicalSort(graph)\)
Input: A directed graph \(G = (V, E)\)
Output: Topological order of vertices or a message indicating a cycle
- Initialize \(InDegree\) as an array of size \(|V|\) with all values set to \(0\).
- Initialize \(Sorted\) as an empty list.
- Initialize \(Queue\) as an empty queue.
- For each vertex \(u\) in \(V\):
- For each neighbor \(v\) of \(u\):
- Increment \(InDegree[v]\) by \(1\).
- For each neighbor \(v\) of \(u\):
- For each vertex \(u\) in \(V\):
- If \(InDegree[u] == 0\):
- Enqueue \(u\) into \(Queue\).
- If \(InDegree[u] == 0\):
- While \(Queue\) is not empty:
- Dequeue \(u\) from \(Queue\).
- Add \(u\) to \(Sorted\).
- For each neighbor \(v\) of \(u\):
- Decrement \(InDegree[v]\) by \(1\).
- If \(InDegree[v] == 0\):
- Enqueue \(v\) into \(Queue\).
- If the size of \(Sorted\) equals \(|V|\):
- Return \(Sorted\).
- Else:
- Return “Graph has a cycle”.
Analysis
The time complexity of Kahn’s algorithm is \(O(V + E)\), where \(V\) is the number of vertices and \(E\) is the number of edges in the graph. The algorithm calculates the in-degree of each vertex in \(O(V + E)\) time, and each vertex is enqueued and dequeued at most once, resulting in a total time complexity of \(O(V + E)\).
The space complexity of Kahn’s algorithm is \(O(V)\), where \(V\) is the number of vertices in the graph. The algorithm maintains an array of in-degrees, a list of the topological ordering, and a queue of vertices with in-degree 0, each requiring \(O(V)\) space.