Hashing Functions
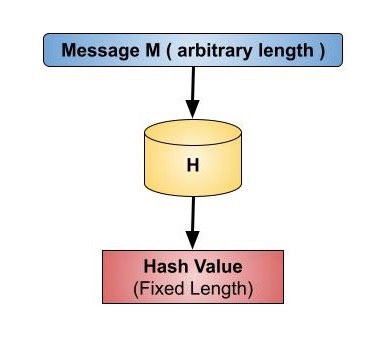
Hash functions are used to map data values (keys) to specific locations in a data structure.
The input to a hash function is a key, which can be of any data type, such as an integer, string, or object.
The output of a hash function is a hash value, which is used to determine the location where the key should be stored in the data structure.

There are many hash functions that use numeric or alphanumeric keys. This article focuses on discussing different hash functions:
- Division Method
- Multiplication Method
- Mid-Square Method
- Folding Method
- Cryptographic Hash Functions
- Universal Hashing
- Perfect Hashing
All of the following hash functions are defined for numeric keys.
Most programming languages provide built-in hash functions that can be used for hashing strings, objects, and other data types.
For example, Java provides the hashCode() method for objects, which can be used to generate hash values for objects. In Python, the hash() function can be used to generate hash values for objects.
These built-in hash functions are designed to produce guarenteed unique hash values for different objects and are optimized for performance. The guarenteed uniqueness of hash values is accomplished by using a combination of the object’s memory address among other properties.
Desired Properties
Some of the desired properties of a good hash function are:
Deterministic: The same input should always produce the same output.
Uniformity: The hash values should be uniformly distributed across the hash table to minimize collisions.
Efficiency: The hash function should be computationally efficient to calculate the hash value quickly.
Consistency: The hash function should produce consistent hash values for the same key.
Avalanche Effect: A small change in the input should produce a significantly different hash value.
Non-reversibility: It should be difficult to reverse-engineer the original input from the hash value.
Collision Resistance: It should be difficult to find two different inputs that produce the same hash value.
Universal Hashing
Universal hashing is a technique that involves selecting a hash function randomly from a family of hash functions. The goal of universal hashing is to minimize collisions and distribute the keys evenly across the hash table.
A family of hash functions is considered universal if, for any two distinct keys \(k_1\) and \(k_2\), the probability that they collide under a randomly chosen hash function is at most \(1/m\), where \(m\) is the size of the hash table.
A common universal hash function is the polynomial hash function, which is defined as:
\[ h(k) = ((a \cdot k + b) \mod p) \mod m \]
Where \(a\) and \(b\) are randomly chosen constants, \(p\) is a prime number greater than \(m\), and \(k\) is the key.
Universal hashing is useful in scenarios where the keys are not known in advance, and the hash function needs to be selected dynamically.
Perfect Hashing
Perfect hashing is a technique that eliminates collisions by guaranteeing that each key maps to a unique hash value. Perfect hashing is useful in scenarios where the keys are known in advance, and the hash function can be optimized for the specific set of keys.
There are two types of perfect hashing:
Static perfect hashing: The hash function is precomputed and optimized for a fixed set of keys. It guarantees no collisions for the given set of keys.
Dynamic perfect hashing: The hash function is computed dynamically based on the keys inserted into the hash table. It adjusts the hash function to minimize collisions as keys are added or removed.
Perfect hashing is used in applications where fast lookup times are critical, such as compilers, databases, and network routers.
Common Hash Functions
Division Method
The division method is the simplest hash function. It involves dividing the key by the table size and taking the remainder as the hash value. The hash function is given by:
\[ h(k) = k\mod m \]
where \(k\) is the key and \(m\) is the size of the hash table. The division method is easy to implement and works well for integer keys.
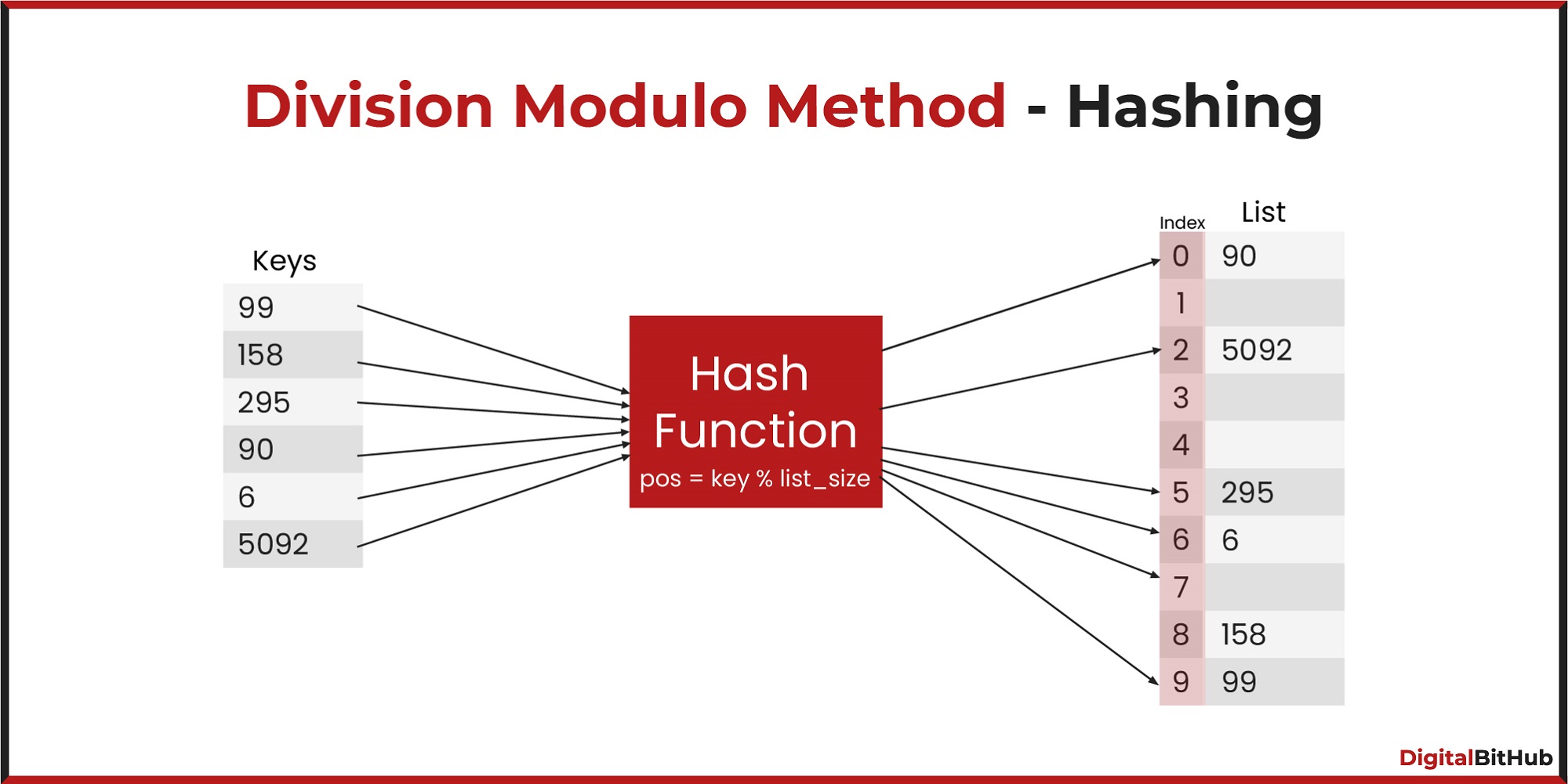
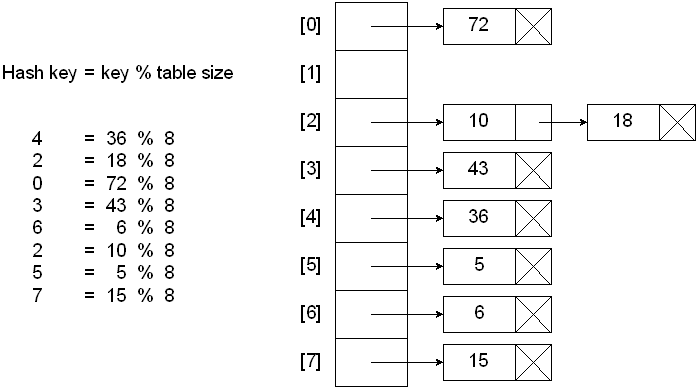
When using the division method, it is important to choose a prime number \(m\) as the size of the hash table to reduce collisions.
Prime numbers are preferred because they have fewer divisors, which can help distribute the keys more evenly across the hash table.
However, it can lead to collisions if the keys are not uniformly distributed.
Multiplication Method
The multiplication method is another simple hash function. It involves multiplying the key by a constant \(A\) and taking the fractional part of the product. The hash function is given by:
\[ h(k) = \lfloor m \cdot (k \cdot A \mod 1) \rfloor \]
where \(k\) is the key, \(m\) is the size of the hash table, and \(A\) is a constant in the range \((0,1)\).
\(A \mod 1\) is the fractional part of \(A\), and the multiplication is done using floating-point arithmetic.

When using the multiplication method, it is important to choose a good constant \(A\) to minimize collisions. A common choice for \(A\) is the golden ratio \((\sqrt{5}-1)/2\) = 0.6180339887.
The golden ratio is known to produce a good distribution of hash values.
The multiplication method is more effective than the division method in avoiding collisions.
Mid-Square Method
The mid-square method is a hash function that involves squaring the key, taking the middle digits, and using them as the hash value. The hash function is given by:
\[ h(k) = \text{middle}(k^2) \]
where \(k\) is the key and \(\text{middle}(x)\) returns the middle digits of \(x\).
The middle digits are selected based on the size of the hash table. For example, if the hash table size is 1000, the middle three digits of the square are used.

Mid-square function is known to produce a good distribution of hash values but can be computationally expensive for large keys.
Compared to the division and multiplication methods, the mid-square method is less commonly used.
Folding Method
The folding method is a hash function that involves dividing the key into equal-sized parts, adding them together, and taking the remainder as the hash value. The hash function is given by:
\[ h(k) = (k_1 + k_2 + \ldots + k_n) \mod m \]
where \(k\) is the key, \(k_i\) are the parts of the key, \(m\) is the size of the hash table, and \(n\) is the number of parts.
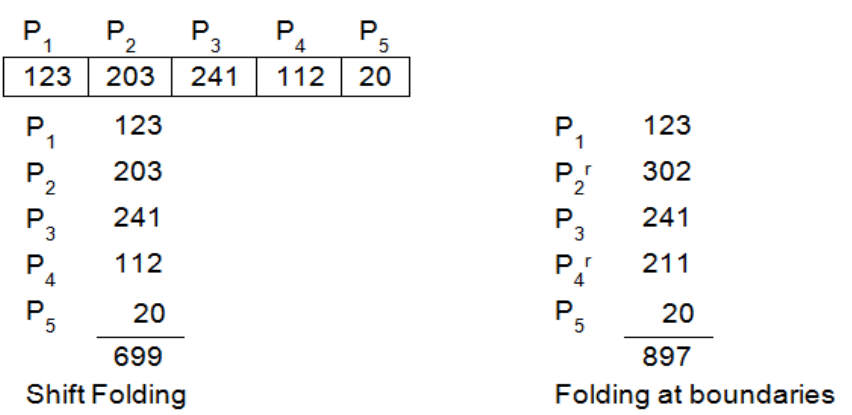
The folding method is useful for keys that are longer than the hash table size. It breaks down the key into smaller parts and combines them to generate the hash value.
The folding method can be used with different folding techniques, such as folding by digits, folding by characters, or folding by groups of digits.
Cryptographic Hash Functions
Cryptographic hash functions are hash functions that are designed to be secure and resistant to attacks. They are used in cryptography to generate hash values for digital signatures, message authentication codes, and password hashing.
How MD5 Processes Data:
MD5 is a cryptographic hash function that applies a series of mathematical operations to transform the input into a fixed-length output (128-bit hash). Here’s a step-by-step breakdown:
Input Data Preparation: Break the input data into 512-bit blocks (64 bytes each). If the data isn’t a multiple of 512 bits, pad it by appending a ‘1’ bit, followed by enough ‘0’ bits, and finally append the original length of the data in bits as a 64-bit value.
Initialize MD5 State Variables: Use four 32-bit state variables (A, B, C, D) initialized to predefined constants. These variables will hold intermediate and final hash values.
Iterative Hash Computation: For each 512-bit block, perform four rounds of non-linear functions and bitwise operations (like AND, OR, XOR, rotations) on the state variables using the block’s data. After processing all blocks, combine the state variables to produce the final 128-bit hash output.