Minimum Spanning Trees

Spanning Tree

A spanning tree of a connected graph $G(V, E)$ is a subgraph $G'$, containing all the vertices $V$ and a subset of the edges $E$, that is a tree and connects all the vertices together.

Formally, $G'(V, E')$ is a spanning tree of $G(V, E)$ if $E' \subseteq E$ and $G'$ is a tree.

The number of edges in a spanning tree is always $V - 1$, where $V$ is the number of vertices in the graph.

Note that the key distinction between trees and graphs is that trees are acyclic, while graphs can have cycles. Therefore, by definition, a spanning tree must be acyclic and connected (i.e., there is a path between every pair of vertices).

Spanning Tree is not defined for disconnected graphs.

Note that a graph can have multiple spanning trees, depending on which edges are included in the subgraph.

Minimum Spanning Tree

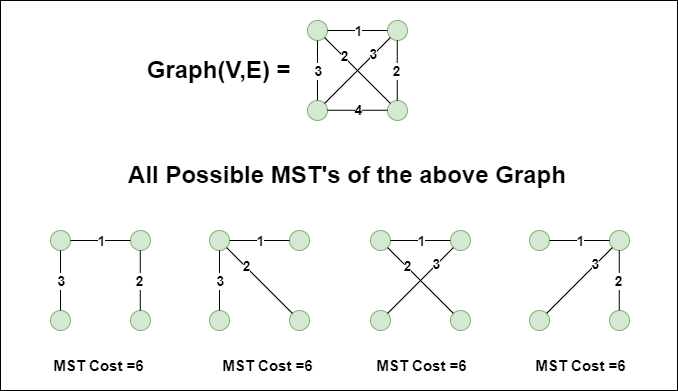
A minimum spanning tree (MST) of a connected graph is a subgraph that is a tree and connects all the vertices together with the minimum possible total edge weight.

Formally, MST of a graph $G(V, E)$ is a spanning tree $G'(V, E')$ such that the sum of the weights of the edges $\sum_{e \in E'} w(e)$ is minimized.

For a graph with $ |V| = n $ vertices, the MST will have $ n - 1 $ edges.

MST is not unique, and a graph can have multiple MSTs if there are multiple edges with the same weight.

Cut Property

The cut property is a key property that helps in understanding the construction of minimum spanning trees.

Given a graph $G(V, E)$ and a partition of the vertices $V$ into two sets $S_1$ and $S_2$, a cut is a set of edges that have one endpoint in $S_1$ and the other endpoint in $S_2$.

For any cut $(S_1, S_2)$ of the graph, if an edge $e$ has the minimum weight among all the edges that cross the cut, then this edge $e$ must be part of the minimum spanning tree of the graph.

This property is crucial in the design of algorithms for finding minimum spanning trees, such as Kruskal’s algorithm and Prim’s algorithm.

Applications

Network Design and Routing: Finding the minimum cost network that connects all the nodes. For example, laying cables to connect all houses with minimum cost or designing a circuit with minimum cost that connects all components.

Cluster Analysis and Image Segmentation: The minimum spanning tree can be used to identify clusters of data points, where the edges represent say euclidean distance between points. The tree can be “cut” at high cost edges to get desired number of clusters.