Implementations
There are several ways to implement a graph, each with its own advantages and disadvantages. The choice of implementation depends on the specific requirements of the application, such as the number of vertices and edges, the operations to be performed on the graph, and the memory constraints.
Four common ways to represent a graph are:
| Representation | Description | Space Complexity |
|---|---|---|
| 1. Adjacency Matrix | A 2D array of size \(V \times V\) where \(V\) is the number of vertices in the graph. | \(O(V^2)\) |
| 2. Adjacency List | An array of lists where each list represents the neighbors of a vertex. | \(O(V + E)\) |
| 3. Edge List | A list of all the edges in the graph. | \(O(E)\) |
| 4. Incidence Matrix | A 2D array of size \(V \times E\) where \(V\) is the number of vertices and \(E\) is the number of edges. | \(O(V \times E)\) |
Adjacency Matrix
An adjacency matrix is a 2D array of size \(V \times V\), where \(V\) is the number of vertices in the graph. If the value of the matrix element at row \(i\) and column \(j\) is 1, it indicates an edge between vertices \(i\) and \(j\). For weighted graphs, the matrix can store the weight of the edge instead of 1.

There are two types of adjacency matrices:
Unweighted Graphs: The matrix elements are 0 or 1, indicating the absence or presence of an edge.
Weighted Graphs: The matrix elements are the weights of the edges.
Similarly, for directed graphs, the adjacency matrix can be asymmetric, with different values for the in-degree and out-degree.
Adjacency matrices are useful for dense graphs, where the number of edges is close to the maximum possible number of edges.
Adjacency List
An adjacency list is a collection of lists or arrays used to represent the graph. Each vertex has a list of adjacent vertices. This representation is more space-efficient than an adjacency matrix for sparse graphs.
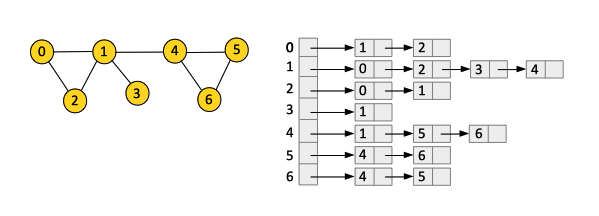
In an adjacency list:
For an undirected graph, each edge \((u, v)\) is stored twice: once in the list of \(u\) and once in the list of \(v\).
For a directed graph, the edge \((u, v)\) is stored only in the list of \(u\).
Adjacency lists are useful for sparse graphs, where the number of edges is much less than the maximum possible number of edges.
Edge List
An edge list is a list of all the edges in the graph. Each edge is represented as a tuple \((u, v)\), where \(u\) and \(v\) are the vertices connected by the edge. For weighted graphs, the tuple can include the weight of the edge.
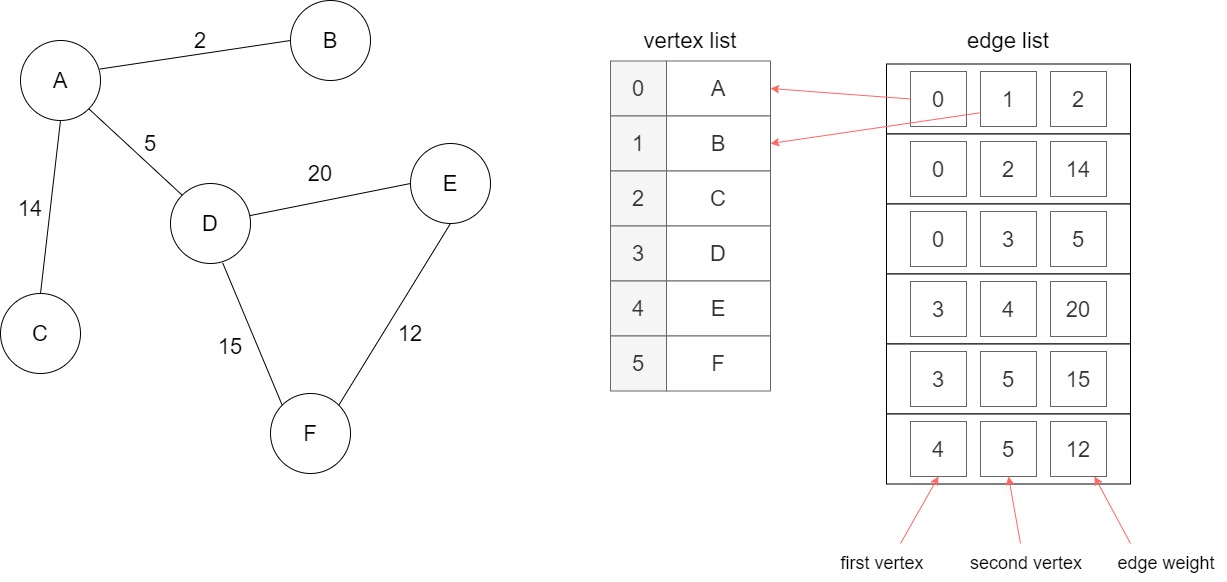
Edge lists are useful for algorithms that require iterating over all the edges of the graph.
Incidence Matrix
An incidence matrix is a 2D array of size \(V \times E\), where \(V\) is the number of vertices and \(E\) is the number of edges in the graph. Each row represents a vertex, and each column represents an edge. The matrix elements indicate the incidence of a vertex in an edge.

Incidence matrices are useful for bipartite graphs and network flow problems.