Traversals
Breadth-First Search (BFS)
Breadth-first search (BFS) is a graph traversal algorithm that explores all vertices at the current depth before moving to the vertices at the next depth.
BFS for a graph is similar to BFS for a tree. The main difference is that:
nodes in a graph can have multiple parents, whereas nodes in a tree have only one parent. So, we need to keep track of the parent of each node to reconstruct the path from the starting node to the target node.
trees are acyclic, so we do not need to keep track of visited vertices, whereas graphs can contain cycles, so we may visit the same vertex again. To avoid processing a vertex more than once, we use a boolean array to mark the visited vertices.
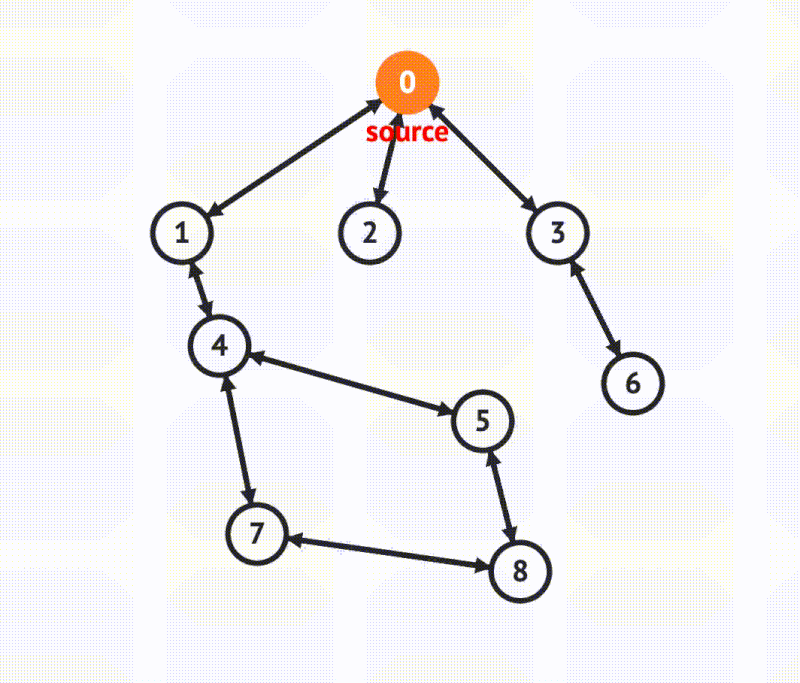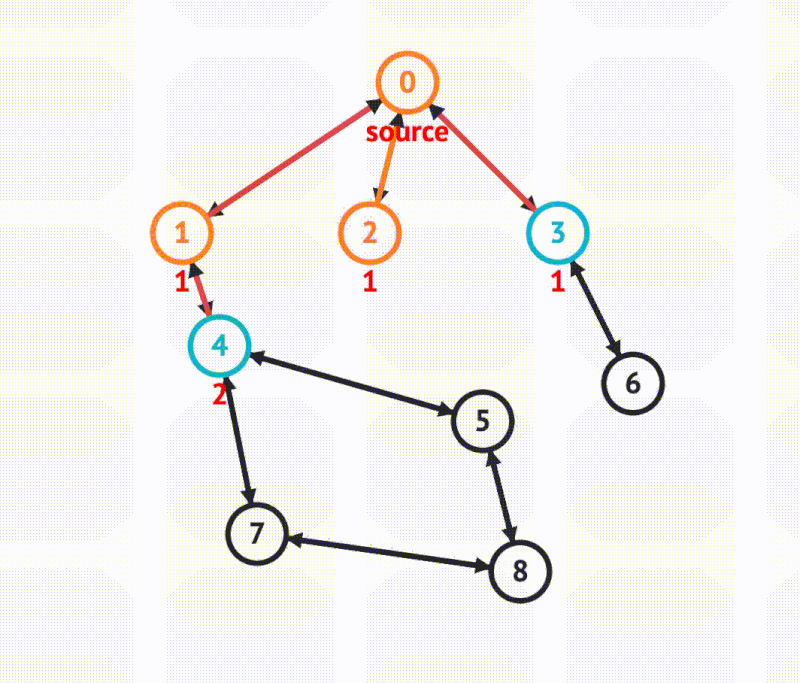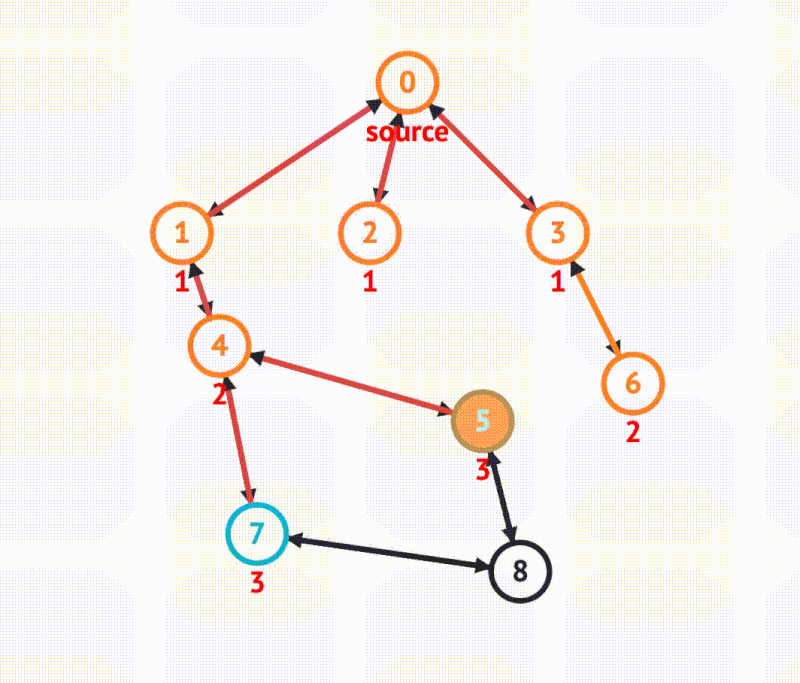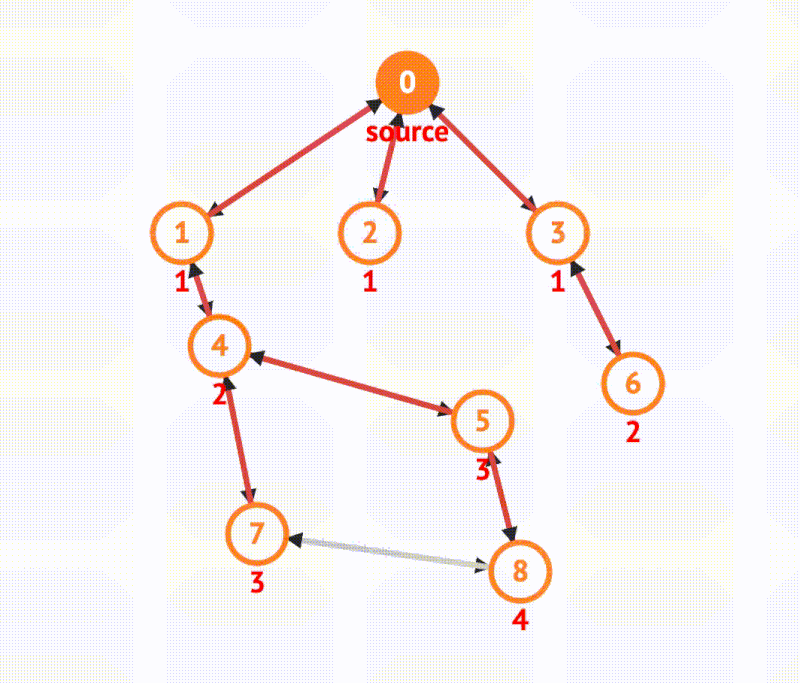
The steps of BFS are as follows:
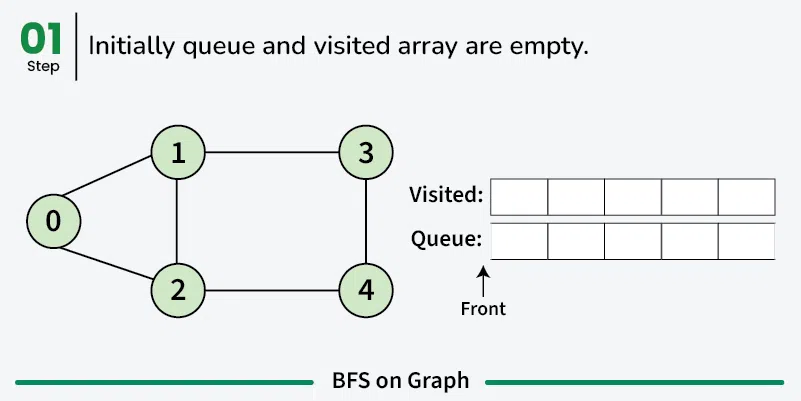
Initialize a queue to store vertices to visit and a set to store visited vertices.
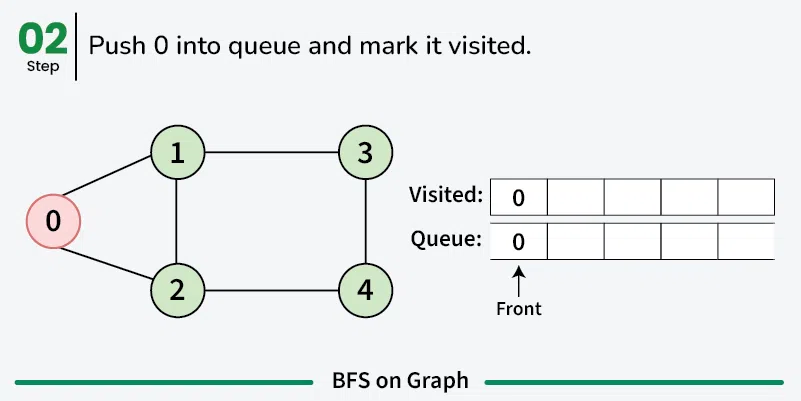
Enqueue the starting vertex into the queue and mark it as visited.
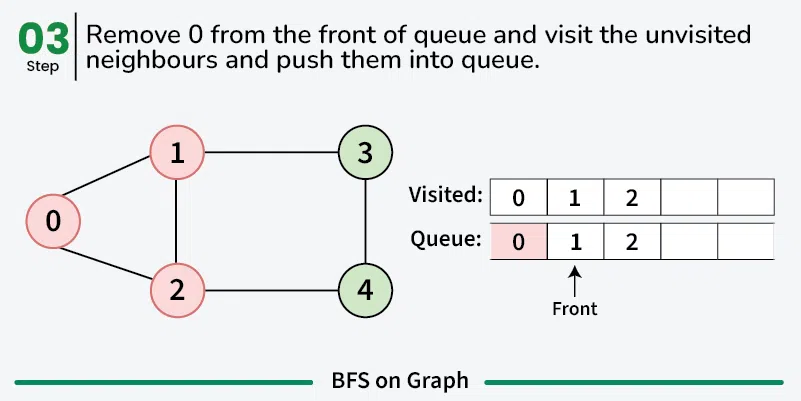
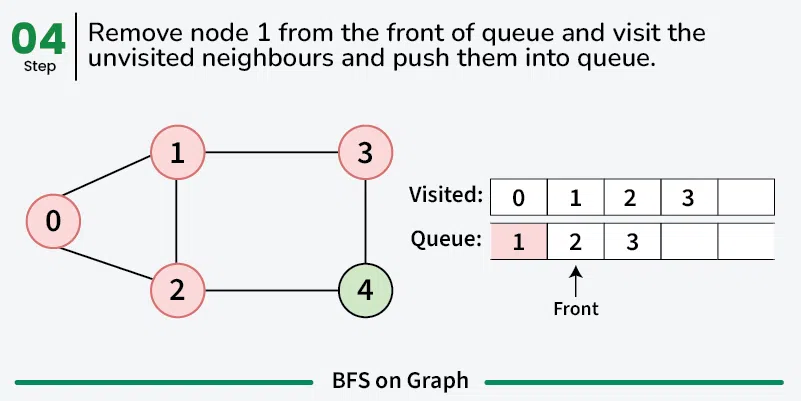
While the queue is not empty:
- Dequeue a vertex from the queue.
- For each neighbor of the dequeued vertex that has not been visited:
- Enqueue the neighbor into the queue and mark it as visited.
- Record the parent of the neighbor (the vertex from which it was reached).
Once the target vertex is reached, reconstruct the path from the starting vertex to the target vertex using the recorded parents.
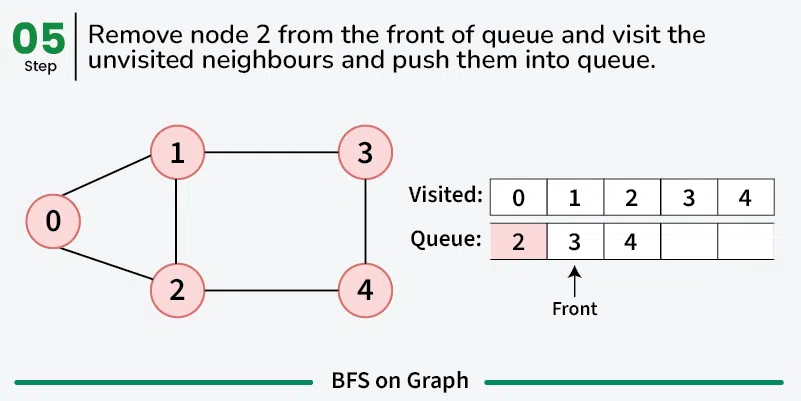
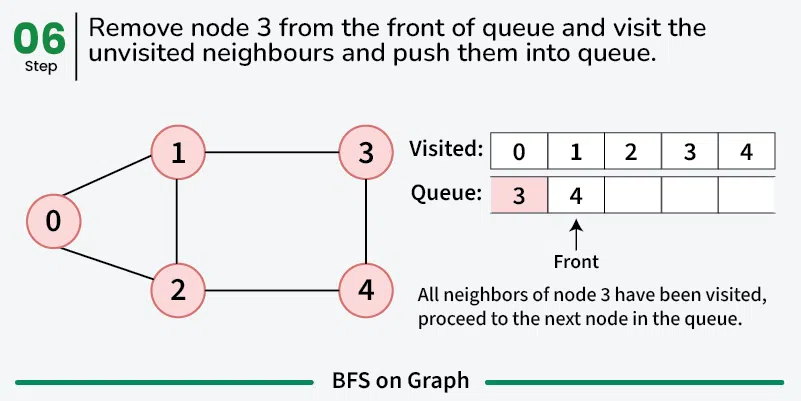
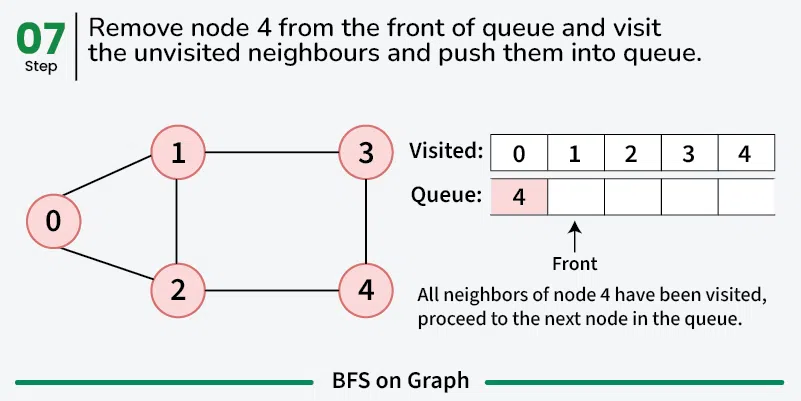
The time complexity of BFS is O(V + E), where V is the number of vertices and E is the number of edges in the graph.
Similar to BFS for a tree, BFS for a graph uses a Queue internally to keep track of the vertices to visit next.
The additional data structure used in BFS for a graph is a boolean array to keep track of visited vertices.
The time complexity of BFS for a graph is \(O(V + E)\), where \(V\) is the number of vertices and \(E\) is the number of edges in the graph.
The space complexity of BFS for a graph is \(O(V)\), where \(V\) is the number of vertices in the graph.
Depth-First Search (DFS)
DFS is an algorithm that explores as far as possible along each branch before backtracking.
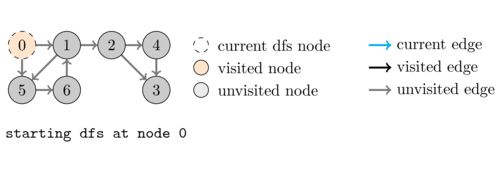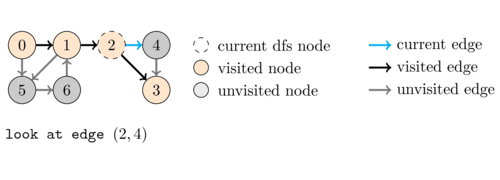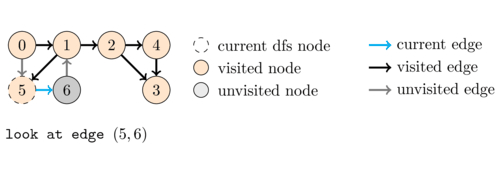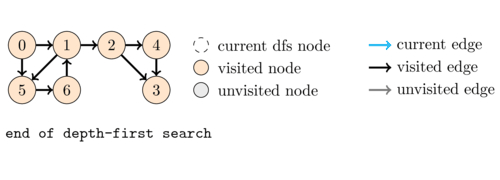
It uses a stack to keep track of the vertices to visit next. The pseudocode for DFS is as follows:
- Start at a vertex \(v\) and mark it as visited.
- Recursively visit all adjacent vertices of \(v\) that have not been visited.
- Repeat step 2 for each unvisited adjacent vertex.
The time complexity of DFS for a graph is \(O(V + E)\), where \(V\) is the number of vertices and \(E\) is the number of edges in the graph.
Applications of Graph Traversals
Graph traversals are fundamental algorithms in graph theory and have many applications, including:
- Pathfinding algorithms like Dijkstra’s algorithm and A* search algorithm.
- Network analysis and routing algorithms.
- Topological sorting algorithms.
- Detecting cycles in a graph.
Finding Cycle in a Graph
A cycle in a graph is a path that starts and ends at the same vertex. Detecting cycles in a graph is an important problem in graph theory and has many applications, such as deadlock detection in operating systems, cycle detection in resource allocation, and detecting negative cycles in financial transactions.

To detect cycles in a graph, we can use the Depth-First Search (DFS) algorithm. The idea is to maintain a boolean array visited to keep track of the vertices visited during the DFS traversal. If we encounter a vertex that is already visited and is not the parent of the current vertex, then there is a cycle in the graph.
Finding Connected Components in a Graph
Connected components in a graph are subgraphs in which every pair of vertices is connected by a path. To find connected components in a graph, we can use either Depth-First Search (DFS) or Breadth-First Search (BFS).
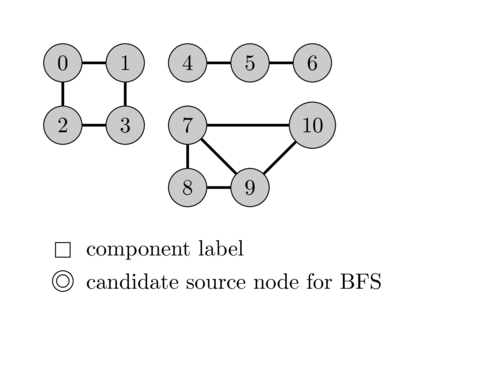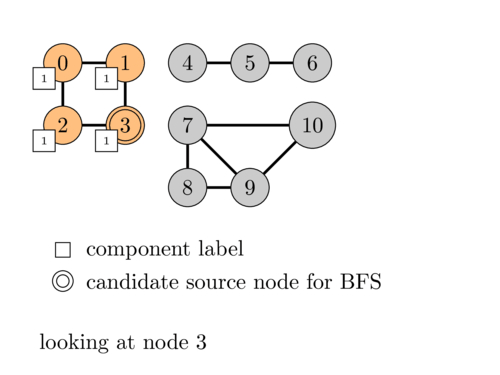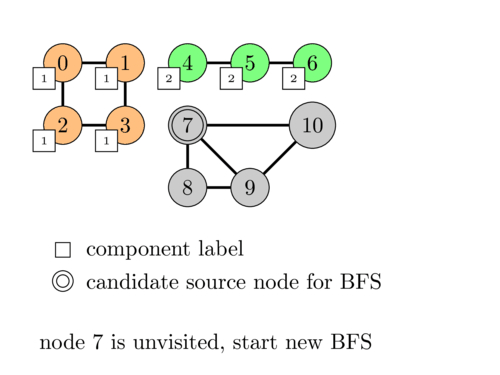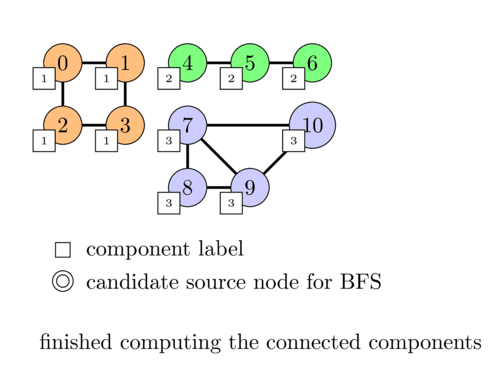
The idea is to start a traversal from each unvisited vertex and mark all the vertices reachable from that vertex. The number of times we start a traversal is the number of connected components in the graph.