Binary Tree
Binary trees are a type of tree data structure in which each node has at most two children, referred to as the left child and the right child.
Properties of a Binary Tree
Trees have the following properties:
A tree with \(n\) nodes has \(n-1\) edges.
A tree with \(n\) nodes has \(n - 1\) edges because of its fundamental properties: it is a connected and acyclic graph.
Starting with a single node and no edges, each additional node requires exactly one edge to connect it to the existing tree, ensuring connectivity without forming cycles. This process continues as the tree grows, with each new node adding exactly one edge. As a result, a tree with \(n\) nodes will always have \(n - 1\) edges.
Nodes (\(n\)) Edges (\(n-1\)) 1 0 2 1 3 2 4 3 … … n n-1 This can also be proven by induction, where adding one node to a tree with \(k\) nodes (and \(k - 1\) edges) leads to \(k\) edges.
The maximum number of nodes at level \(l\) of a binary tree is \(2^l\)
Here level is the number of edges from the root to the node. The level of the root is \(0\).
Level (\(l\)) Maximum Nodes 0 1 1 2 2 4 3 8 … … \(l\) \(2^l\) Each level of the tree doubles the number of nodes from the previous level. The root node is at level 0, and each subsequent level has twice as many nodes as the previous level. Therefore, the maximum number of nodes at level \(l\) is \(2^l\).
A tree with height \(h\) has at most \(2^{h+1} - 1\) nodes.
Each level of the tree doubles the number of nodes from the previous level. The root node is at level 0, and each subsequent level has twice as many nodes as the previous level. Therefore, the total number of nodes in a binary tree of height h is the sum of the nodes at each level, which is given by the formula \(2^0 + 2^1 + ... + 2^(h-1) = 2^{h+1} -1\) .
Height (\(h\)) Maximum Nodes 0 1 1 3 2 7 3 15 … … \(h\) \(2^{h+1} - 1\) Some textbooks count the height of a tree as the number of nodes on the longest path from the root to a leaf node. In that case, the maximum number of nodes in a tree of height h is \(2^h - 1\) .
The height of a binary tree with \(n\) nodes is \(log_2(n+1) - 1\).
The height of a binary tree with \(n\) nodes is \(log(n+1) - 1\) . This formula calculates the height of a binary tree based on the number of nodes it contains. The height of a binary tree is the length of the longest path from the root to a leaf node. By using the formula \(log(n+1) - 1\) , we can determine the height of a binary tree given the number of nodes it contains.
Nodes (\(n\)) Height 1 0 2 1 3 1 4 2 … … n \(log_2(n+1) - 1\) Some textbooks count the height of a tree as the number of nodes on the longest path from the root to a leaf node. In that case, the height of a binary tree with \(n\) nodes is \(log_2(n) + 1\) .
Traversals
Traversal is the process of visiting each node in the tree in a specific order.
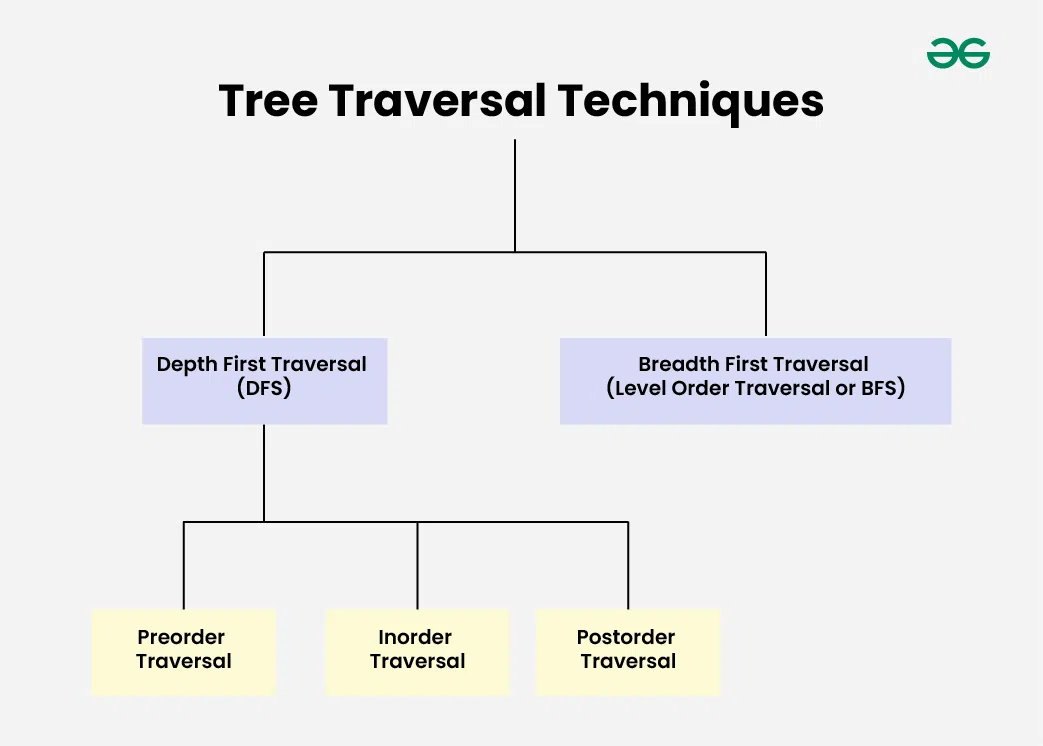
There are two main types of tree traversal:
- Breadth-First Traversal (BFS): A traversal algorithm that explores all the nodes at the present depth before moving on to the nodes at the next depth.
Breadth-first traversal is also known as level-order traversal.
- Depth-First Traversal (DFS): A traversal algorithm that explores as far as possible along each branch before backtracking.
Depth-first traversal includes three types of traversals: preorder, inorder, and postorder.
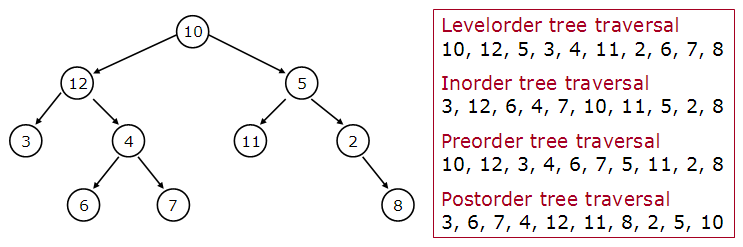
Level Order Traversal (Breath-First Traversal)
Level-order traversal is a breadth-first search (BFS) algorithm that visits all the nodes at the present depth before moving on to the nodes at the next depth.
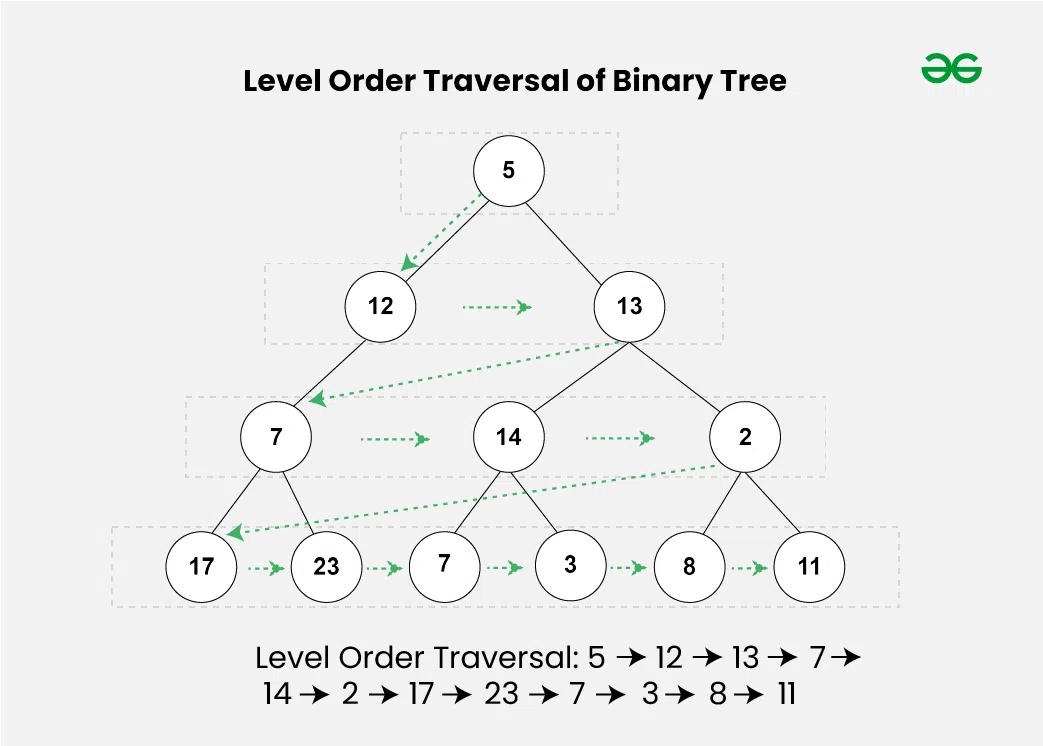
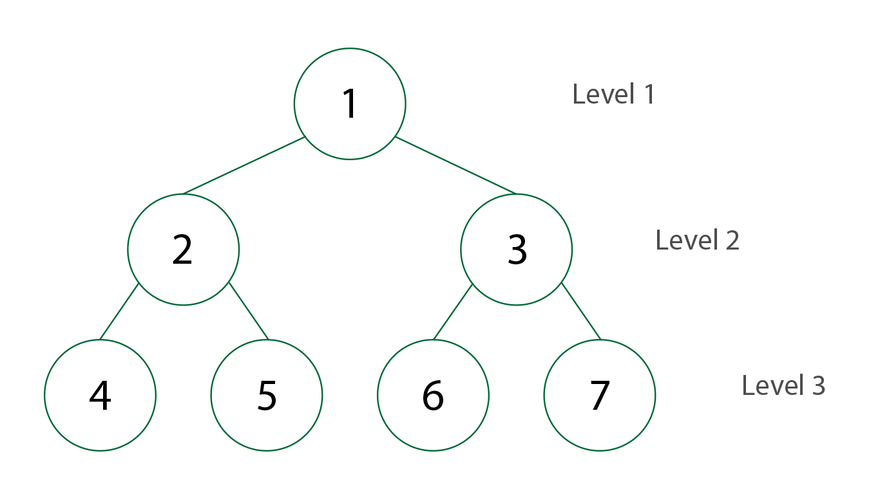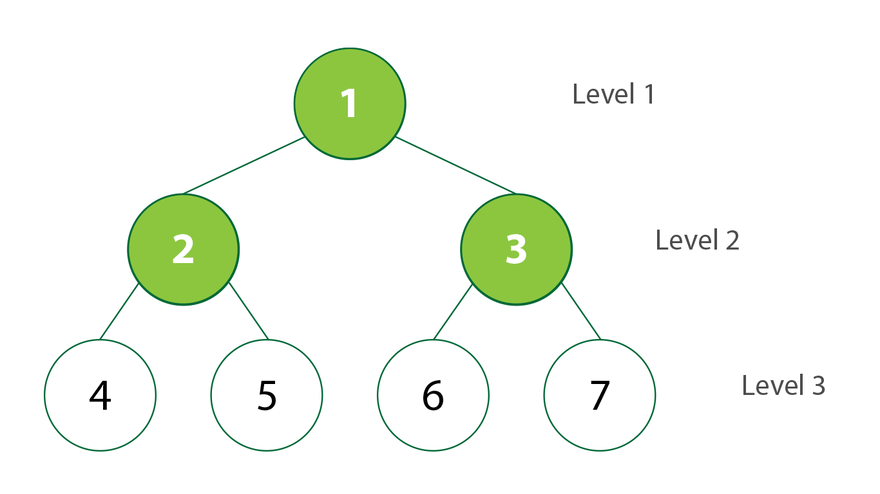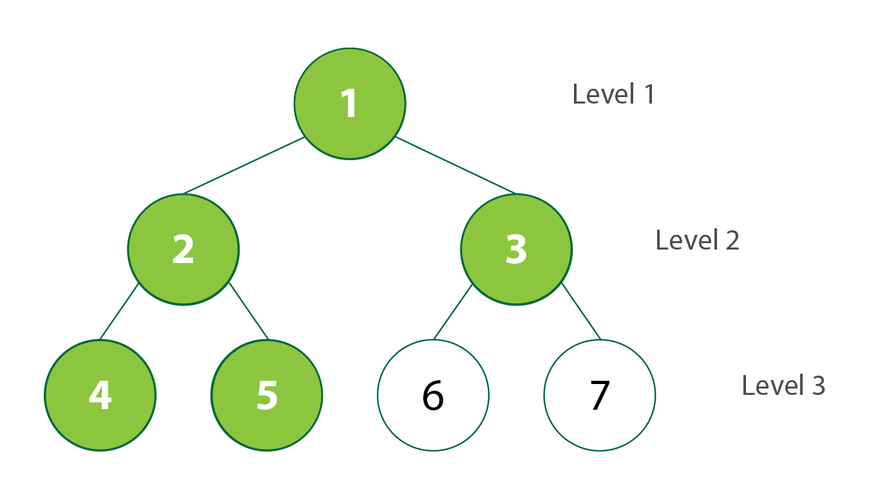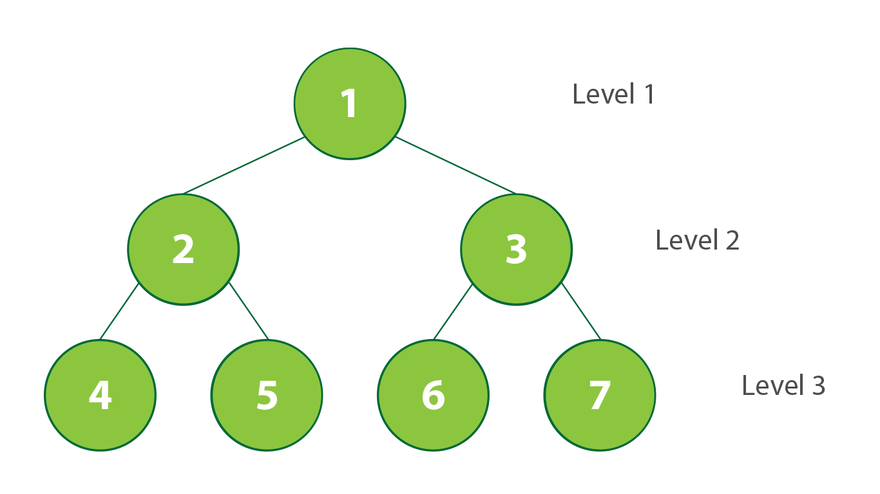
Psuedocode for level order traversal:
- Create a queue and enqueue the root node.
- While the queue is not empty:
2.1. Dequeue a node from the queue.
2.2. Process the node (e.g., print its value).
2.3. Enqueue the left child of the node if it exists.
2.4. Enqueue the right child of the node if it exists.
The time complexity of level order traversal is \(O(n)\), where \(n\) is the number of nodes in the binary tree.
The space complexity of level order traversal is \(O(n)\), where \(n\) is the number of nodes in the binary tree.
Preorder Traversal (DFS: Root-Left-Right)
Visit the root node first, then recursively do a preorder traversal of the left subtree, followed by a preorder traversal of the right subtree.
The preorder traversal of a binary tree is a depth-first traversal that visits the root node first, followed by the left subtree and then the right subtree.
The pseudocode for preorder traversal is as follows:
- Visit the root node.
- Recursively do a preorder traversal of the left subtree.
- Recursively do a preorder traversal of the right subtree.
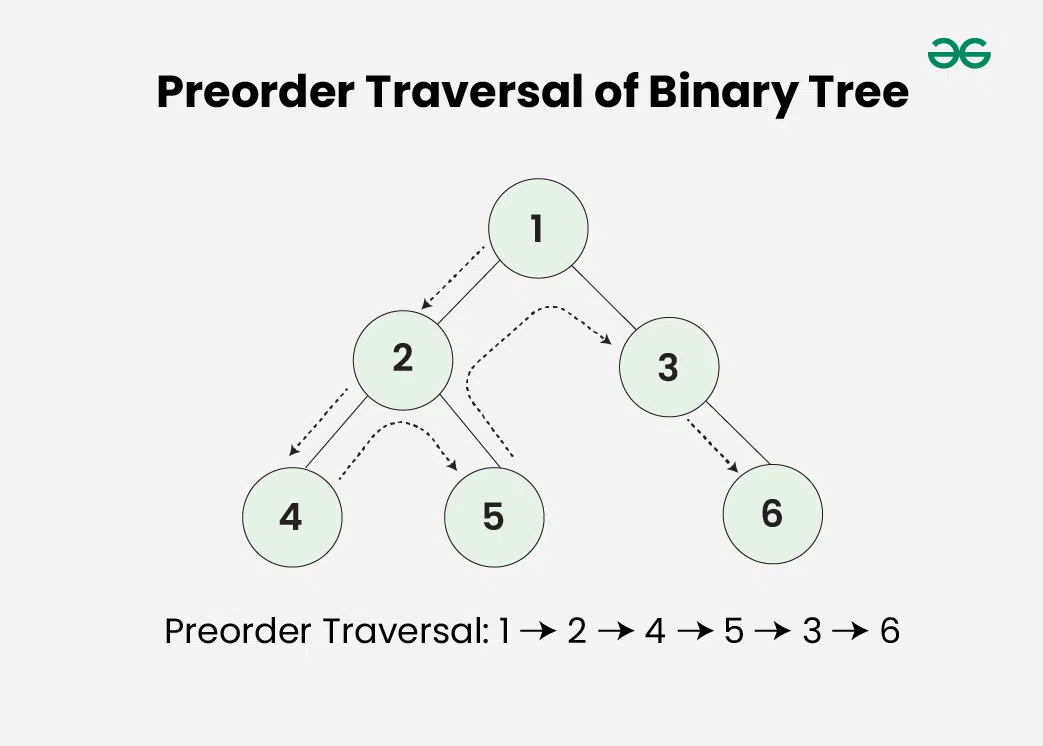

Preorder traversal has the following applications:
Expression Tree: Preorder traversal is used to convert an infix expression to a prefix expression (also known as Polish notation). e.g.,
A + Bto+ A B. Prefix expressions are easier to evaluate using a stack-based algorithm.Clone a Tree: Preorder traversal is used to clone a binary tree. This is because the root node is visited first, making it easy to create a copy of the tree and connecting the left and right subtrees.
In-order Traversal (DFS: Left-Root-Right)
In-order traversal is a depth-first traversal that visits the left subtree first, followed by the root node, and then the right subtree.
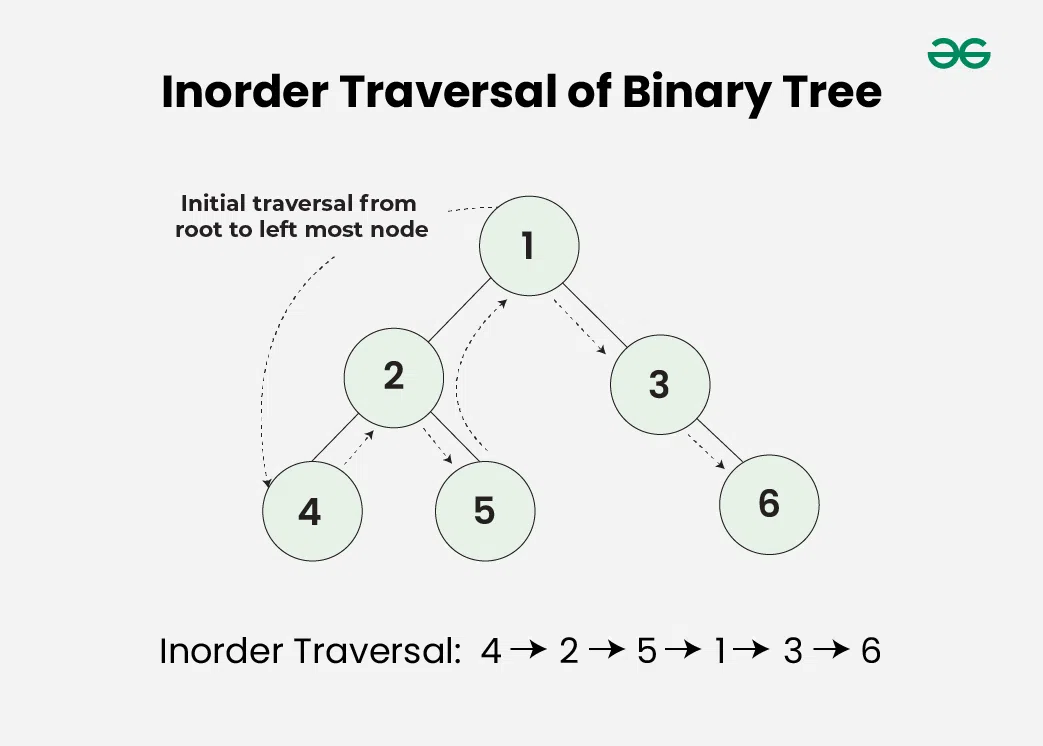

The pseudocode for in-order traversal is as follows:
- Recursively do an in-order traversal of the left subtree.
- Visit the root node.
- Recursively do an in-order traversal of the right subtree.
In-order traversal has the following applications:
Binary Search Tree (BST): In-order traversal of a BST results in a sorted list of elements. This property is used to find the k-th smallest element in a BST.
Postfix Expression and Evaluation: In-order traversal is used to convert an infix expression to a postfix expression (also known as Reverse Polish notation). e.g.,
A + BtoA B +. Postfix expressions are easier to evaluate using a stack-based algorithm.
Post-order Traversal (DFS: Left-Right-Root)
Recursively do a postorder traversal of the left subtree, followed by a postorder traversal of the right subtree, and then visit the root node.
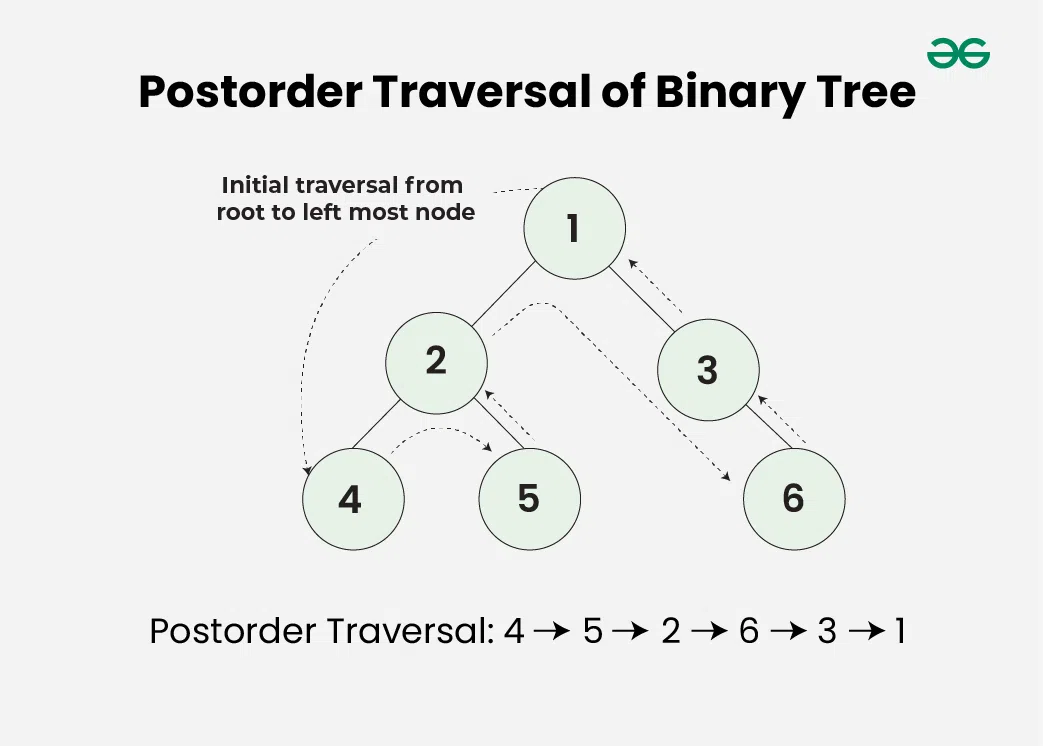

The pseudocode for postorder traversal is as follows:
- Recursively do a postorder traversal of the left subtree.
- Recursively do a postorder traversal of the right subtree.
- Visit the root node.
Postorder traversal has the following applications:
Expression Tree: Postorder traversal is used to convert an infix expression to a postfix expression (also known as Reverse Polish notation). e.g.,
A + BtoA B +. Postfix expressions are easier to evaluate using a stack-based algorithm.Delete a Tree: Postorder traversal is used to delete a binary tree. This is because the root node is visited last, making it easy to delete the tree from the leaves up to the root.
Postorder traversal is commonly used in expression trees to evaluate expressions.
Operations
Insertion
Insertion is the process of adding a new node to the binary tree. The new node is inserted based on the value of the node and the properties of the binary tree.
The pseudocode for inserting a node in a binary tree that is not a binary search tree is as follows:
- Create a new node with the given value.
- If the root is null, set the new node as the root.
- Else, perform a level order traversal to find the first node that has an empty left or right child.
- Insert the new node as the left child if the left child is empty, otherwise insert it as the right child.
The time complexity of inserting a node in a binary tree is \(O(n)\) in the worst case, where \(n\) is the number of nodes in the binary tree.
The space complexity of inserting a node in a binary tree is \(O(n)\) in the worst case, where \(n\) is the number of nodes in the binary tree.
Deletion
Deletion is the process of removing a node from the binary tree. The node to be deleted is removed based on the value of the node and the properties of the binary tree.
The pseudocode for deleting a node in a binary tree is as follows:
- Find the node to be deleted using a level order traversal or any other traversal method.
- If the node has no children, simply remove the node.
- If the node has one child, replace the node with its child.
- If the node has two children, find the inorder successor or predecessor of the node.
- Replace the node with the inorder successor or predecessor.
The time complexity of deleting a node in a binary tree is \(O(n)\) in the worst case, where \(n\) is the number of nodes in the binary tree.
The space complexity of deleting a node in a binary tree is \(O(n)\) in the worst case, where \(n\) is the number of nodes in the binary tree.
Searching
Searching is the process of finding a specific node in the binary tree based on its value.
The pseudocode for searching a node in a binary tree is as follows:
- Perform a level order traversal or any other traversal method to search for the node.
- If the node is found, return the node.
- If the node is not found, return null.
The time complexity of searching for a node in a binary tree is \(O(n)\) in the worst case, where \(n\) is the number of nodes in the binary tree.
The space complexity of searching for a node in a binary tree is \(O(n)\) in the worst case, where \(n\) is the number of nodes in the binary tree.