GRAPHS

A graph is a data structure that consists of a finite set of vertices (nodes) and a collection of edges that connect pairs of vertices. Graphs are used to model relationships between objects, such as cities connected by roads, friends connected by social networks, or dependencies between tasks in a project.

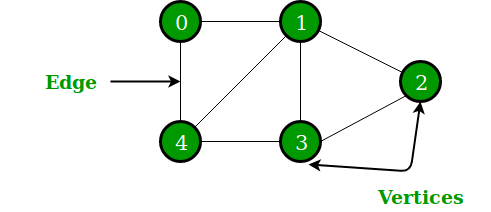
Graph Terminology

• Vertex (Node): A fundamental unit of a graph. It represents an entity, such as a city, person, or object.

• Edge: A connection between two vertices. It represents a relationship between the entities represented by the vertices.

• Directed Graph (Digraph): A graph in which the edges have a direction associated with them. The edges are ordered pairs of vertices.

• Undirected Graph: A graph in which the edges do not have a direction associated with them. The edges are unordered pairs of vertices.

• Weighted Graph: A graph in which each edge has an associated weight or cost. The weight can represent distance, time, cost, or any other relevant metric.

• Path: A sequence of vertices connected by edges. It represents a route from one vertex to another.

• Cycle: A path that starts and ends at the same vertex.

• Connected Graph: A graph in which there is a path between every pair of vertices.

• Disconnected Graph: A graph in which there are vertices that are not connected by any path.

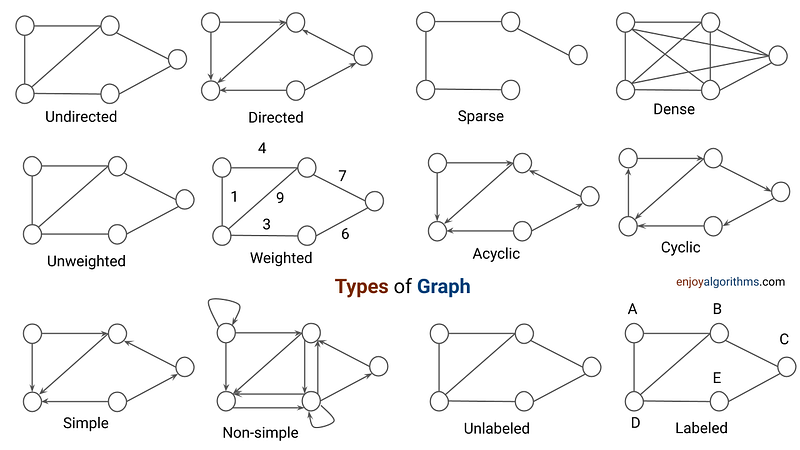
• Degree of a Vertex: The number of edges incident to a vertex. In a directed graph, the degree is divided into the in-degree (number of incoming edges) and out-degree (number of outgoing edges).

• Adjacency: Two vertices are adjacent if there is an edge connecting them.

• Adjacency Matrix: A matrix representation of a graph in which the rows and columns correspond to vertices, and the entries indicate whether an edge exists between the vertices.

• Adjacency List: A list representation of a graph in which each vertex has a list of adjacent vertices.

Graph Representation

There are two common ways to represent a graph: adjacency matrix and adjacency list.