Dijkstra’s Algorithm

Dijkstra’s algorithm is a single-source shortest path algorithm that finds the shortest path from a source vertex to all other vertices in a weighted graph.

A limitation of Dijkstra’s algorithm is that it does not work with negative edge weights.

How it Works

How it works:

Set initial distances for all vertices: 0 for the source vertex, and infinity for all the other.
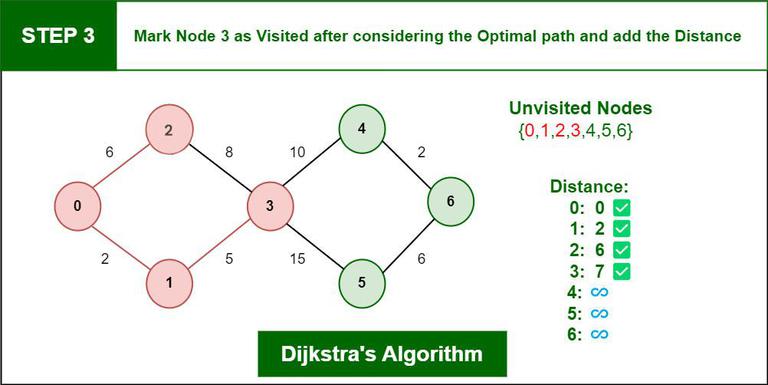
Choose the unvisited vertex with the shortest distance from the start to be the current vertex. So the algorithm will always start with the source as the current vertex.
For each of the current vertex’s unvisited neighbor vertices, calculate the distance from the source and update the distance if the new, calculated, distance is lower.
We are now done with the current vertex, so we mark it as visited. A visited vertex is not checked again.
Go back to step 2 to choose a new current vertex, and keep repeating these steps until all vertices are visited.
In the end we are left with the shortest path from the source vertex to every other vertex in the graph.

Pseudocode

The pseudocode of Dijkstra’s algorithm are as follows:

Initialize the distance to the source vertex as 0 and the distance to all other vertices as infinity.
Create a priority queue to store vertices and their distances from the source vertex.
While the priority queue is not empty:
- Dequeue the vertex with the minimum distance from the priority queue.
- For each neighbor of the dequeued vertex:
  - Calculate the distance to the neighbor through the dequeued vertex.
  - If the new distance is less than the current distance to the neighbor, update the distance and enqueue the neighbor.

Example

Implementation

Here is an implementation of Dijkstra’s algorithm in Java:

// Edge class to represent an edge between two nodes with a weight
private static class Edge implements Comparable<Edge>{
    int source;
    int destination;
    int weight;

    public Edge(int source, int destination, int weight) {
        this.source = source;
        this.destination = destination;
        this.weight = weight;
    }

    // Compare edges based on their weight
    @Override
    public int compareTo(Edge other) {
        return Integer.compare(this.weight, other.weight);
    }
}

import java.util.*;

public class GraphAdjacencyList {
    private int vertices; // Number of vertices
    private List<List<Edge>> adjacencyList; // Adjacency list for the graph

    public GraphAdjacencyList(int vertices) {
        this.vertices = vertices;
        adjacencyList = new ArrayList<>(vertices);
        for (int i = 0; i < vertices; i++) {
            adjacencyList.add(new ArrayList<>());
        }
    }

    // Add an edge to the graph
    public void addEdge(int source, int destination, int weight) {
        adjacencyList.get(source).add(new Edge(source, destination, weight));
    }

    // Dijkstra's algorithm implementation
    public int[] dijkstra(int startVertex) {
        int[] distances = new int[vertices];
        Arrays.fill(distances, Integer.MAX_VALUE);
        distances[startVertex] = 0;

        PriorityQueue<Edge> pq = new PriorityQueue<>();
        pq.add(new Edge(-1, startVertex, 0));

        while (!pq.isEmpty()) {
            Edge current = pq.poll();
            int currentVertex = current.destination;

            for (Edge edge : adjacencyList.get(currentVertex)) {
                int newDist = distances[currentVertex] + edge.weight;
                if (newDist < distances[edge.destination]) {
                    distances[edge.destination] = newDist;
                    pq.add(new Edge(currentVertex, edge.destination, newDist));
                }
            }
        }

        return distances;
    }