TREES

Trees are one of the most important data structures in computer science. They are a non-linear data structure that store data in a hierarchical manner.

Trees offer efficient insertion, deletion, and search operations, making them a versatile data structure for a wide range of applications.

Trees are ubiquitous in computer science and are used for a wide variety of applications, including file systems, parsing languages, and artificial intelligence to plan out strategies and make decisions.

File system	Artificial Intelligence	Parsing Language

Terminology

The tree data structure come with a non-trivial amount of terminology. Here are some of the key terms:

• Nodes: The individual elements in a tree that store data. These are depicted as circles in the diagram. They are very similar to linked list nodes.

• Edges: The connections between nodes. These are depicted as lines in the diagram.

• Root Node: The topmost node in a tree. It is the only node in the tree that has no parent.

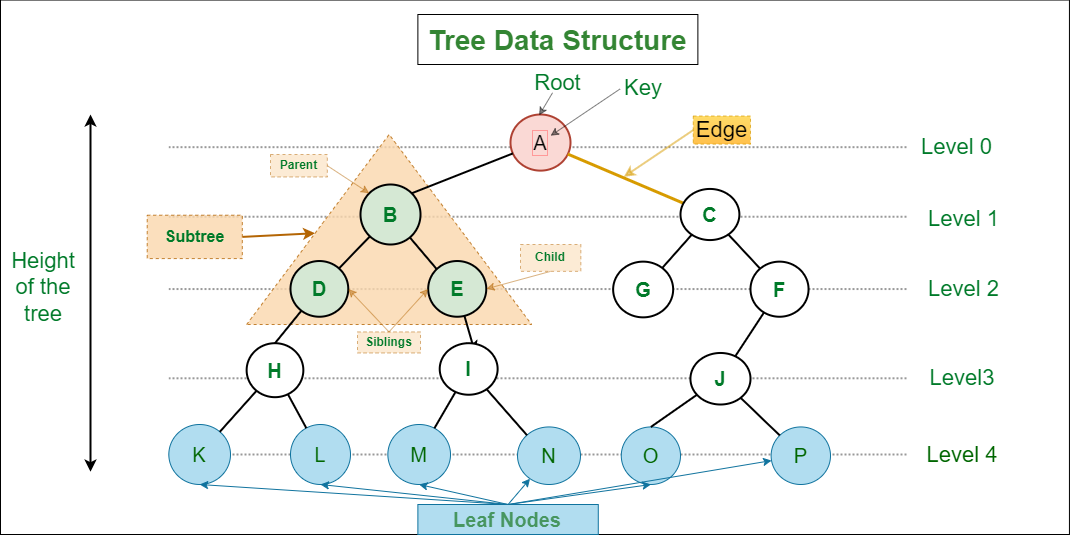
• Parent Node: A node that has child nodes. Each node in the tree, except the root node, has exactly one parent node.

• Child Node: A node that is connected to a parent node. Each node in the tree can have zero or more children.

• Leaf: Nodes that have no child nodes. They are the nodes at the bottom of the tree.

• Path: A sequence of nodes connected by edges.

• Height of a tree: The length of the longest path from the root to a leaf. Length is measured in the number of edges.

• Height of a node: The length of the longest path from the node to a leaf. Length is measured in the number of edges.

• Depth: The length of the path from the root to a node. Length is measured in the number of edges.

• Level: The depth of a node in the tree. The root node is at level 0.

• Subtree: A tree that is part of a larger tree. It consists of a node and all its descendants.

• Internal Node: A node that has at least one child node. Essentially, any node that is not a leaf.

• External Node: A node that has no child nodes. Essentially, a leaf node.

• Sibling: Nodes that share the same parent.

• Ancestors of a node: A node that is on the upward path a given node to the root.

• Descendant of a node: A node that is on the path from a given node to a leaf.

Types of Trees

There are many different types of trees, each with its own unique properties and characteristics. Here we are focusing on types of trees based on the number of children each node can have.

Note that we are going the following mathematical notation for trees:

• \(n\) to represent the number of nodes in the tree,
• \(N\) to represent the maximum number of children each node can have
• \(h\) to represent the height of the tree.

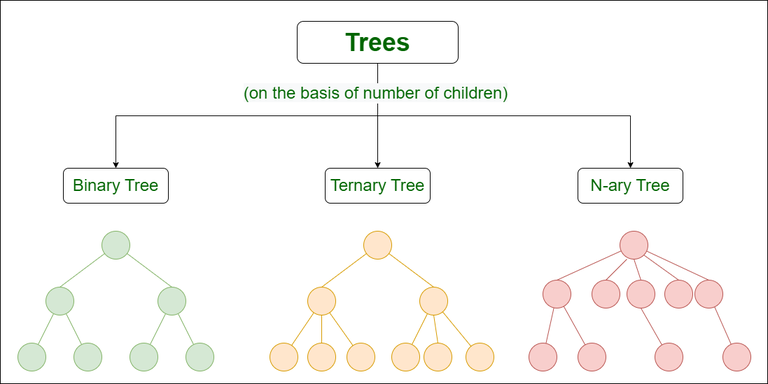
The most common types of trees Binary trees that have at most two children per node. Binary trees are further classified into different types based on their properties.

• Full Tree

  An \(N\)-ary tree in which every node has either zero or \(N\) children.

• Complete Tree

  An \(N\)-ary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.

• Degenerate Tree

  A tree in which each parent node has only one child node. This is essentially a linked list.

• Perfect Tree

  An \(N\)-ary tree in which all interior nodes have \(N\) children and all leaves have the same depth or same level.

• Balanced Tree

  A \(N\)-ary tree in which the heights of all the subtrees of each node differ by at most one.

Properties of Trees

Trees have the following properties:

• Tree Property: A tree with \(n\) nodes has \(n-1\) edges.

  The number of edges in a tree is always one less than the number of nodes.

  This is because each node, except the root node, has exactly one parent node.

• Full Tree Property: An N-ary tree with height \(h\) has at most \(N^h\) nodes.

  A full tree is a tree in which each node has exactly \(N\) children.

• Height Property: The height of an N-ary tree with \(n\) nodes is \(\log_N(n+1) - 1\).

  The height of a tree is the length of the longest path from the root to a leaf.