1. Vectorized Operations on Data

Computer Science is all about getting computers to perform tasks for us efficiently, reliably and correctly.

When we talk about efficiency, we are talking both space (memory) and time (speed).

Given we are living through the data deluge of the 21st century, when working with data, the issues of time and space are particularly relevant.

Let’s talk about speed first.

Time Complexity

Computer scientists are a little paranoid when it comes to speed. We always assume the worst!

Wait, how do we even measure speed?

And what are we even measuring the speed of?

Should we be measuring the amount of time it takes for our code to run?

We know computers are much faster today then they were only a few years ago and my Dad’s computer today is much slower than mine.

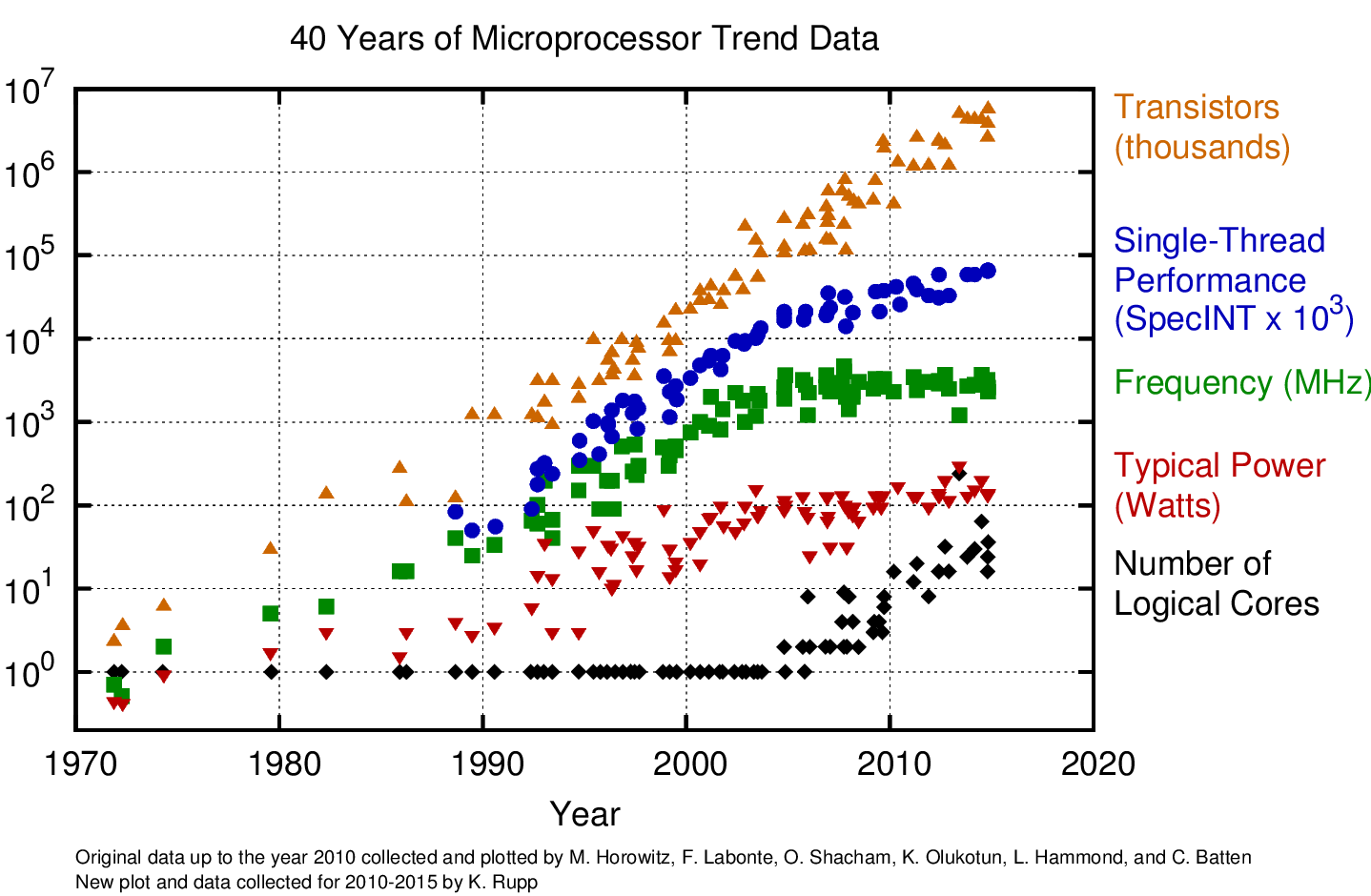
Fig. 1.1 Improvement in Processors over the years

So if we are measuring the speed of a computer program, whose computer should we measure the speed on?

Should we measure speed on an “average computer” available to buy in the market today? Identifying such an average computer sounds like a lot of work!

What do we do when newer faster computers come out in the future?

We also know some programming languages are faster than others.

It sounds like what we need is an abstract theoretical framework for measuring speed that is independent of any particular hardware specifications and any programming language.

Thankfully, this is a solved problem.

Computer Scientists long ago decided to measure speed of an algorithm, as opposed to any particular program in any programming language. An Algorithm if you recall is simply a sequence of instructions that maps inputs to outputs.

Five basic instructions of an algorithm:

1. Input

2. Output

3. Math

4. Branching

5. Repetition

Guess which of the five above is most relevant to measuring speed of an algorithm?

It is number 5: Repetitions! Also known as LOOPS!

That is, in computer science, we measure the speed of an algorithm in terms of iterations of a loop.

If an algorithm does not have any loops in it, it is said to be a constant time algorithm, even if that has a million input/output/math/branching instructions. Algorithms are classified using the big Big O-Notation. A constant time algorithm in O(1).

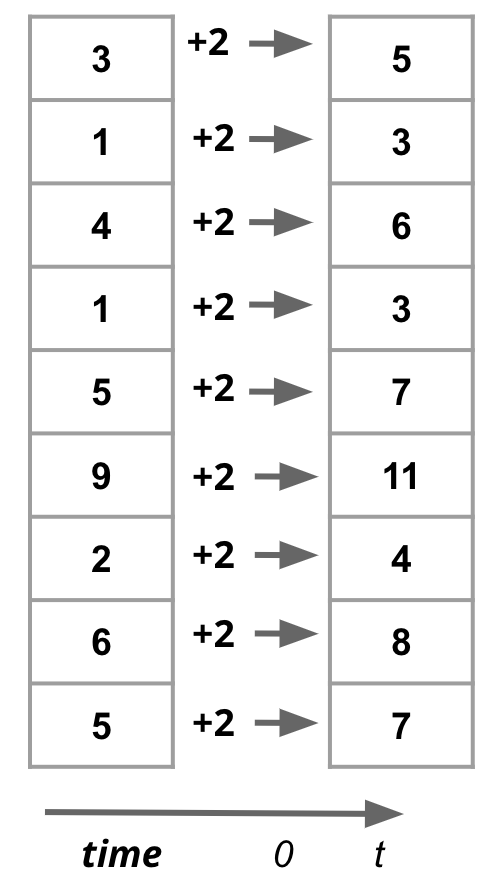
Your average algorithm has atleast one loop that iterates over some particular data structure. So what label do we give to an algorithm with one loop that follows the basic template:

sequence = [3, 1, 4, 1, 5, 9, 2, 6, 5]
i = 0 
while i < len(sequence):
    sequence[i] = sequence[i] + 2
    print(i, sequence)
    i = i + 1

0 [5, 1, 4, 1, 5, 9, 2, 6, 5]
1 [5, 3, 4, 1, 5, 9, 2, 6, 5]
2 [5, 3, 6, 1, 5, 9, 2, 6, 5]
3 [5, 3, 6, 3, 5, 9, 2, 6, 5]
4 [5, 3, 6, 3, 7, 9, 2, 6, 5]
5 [5, 3, 6, 3, 7, 11, 2, 6, 5]
6 [5, 3, 6, 3, 7, 11, 4, 6, 5]
7 [5, 3, 6, 3, 7, 11, 4, 8, 5]
8 [5, 3, 6, 3, 7, 11, 4, 8, 7]

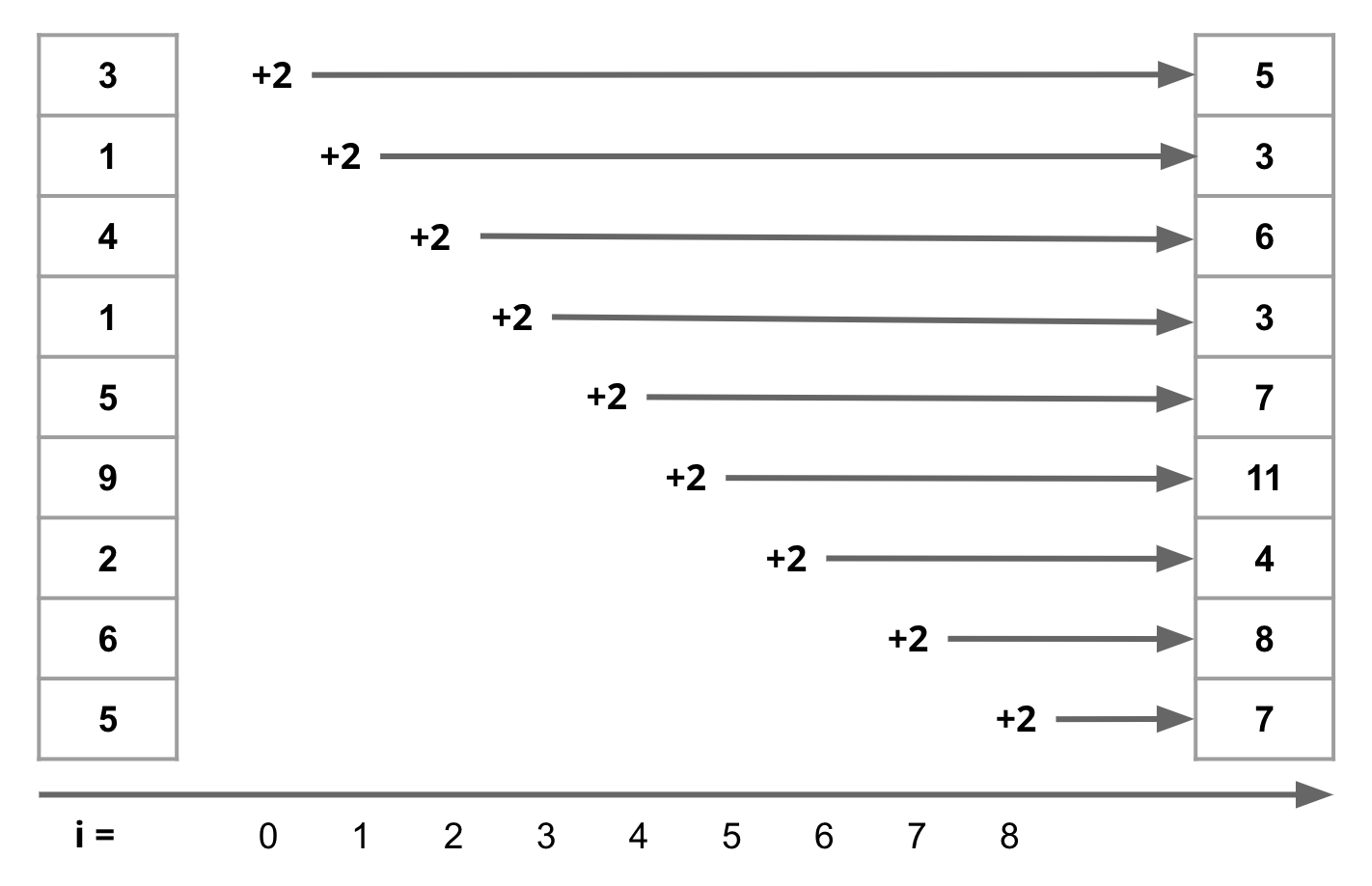
Fig. 1.2 Serial execution of loops: each iteration must wait for the previous one to finish.

Such algorithms are given the label linear time or, in Big-O notation, O(n).

The letter n here is the size of the data structure i.e. len(arr). Length of a data structure also happens to be the number of iterations of the loop.

In summary, we measure the speed of an algorithm in relation to:

• size of data

• number of iterations in all loops in the algorithm

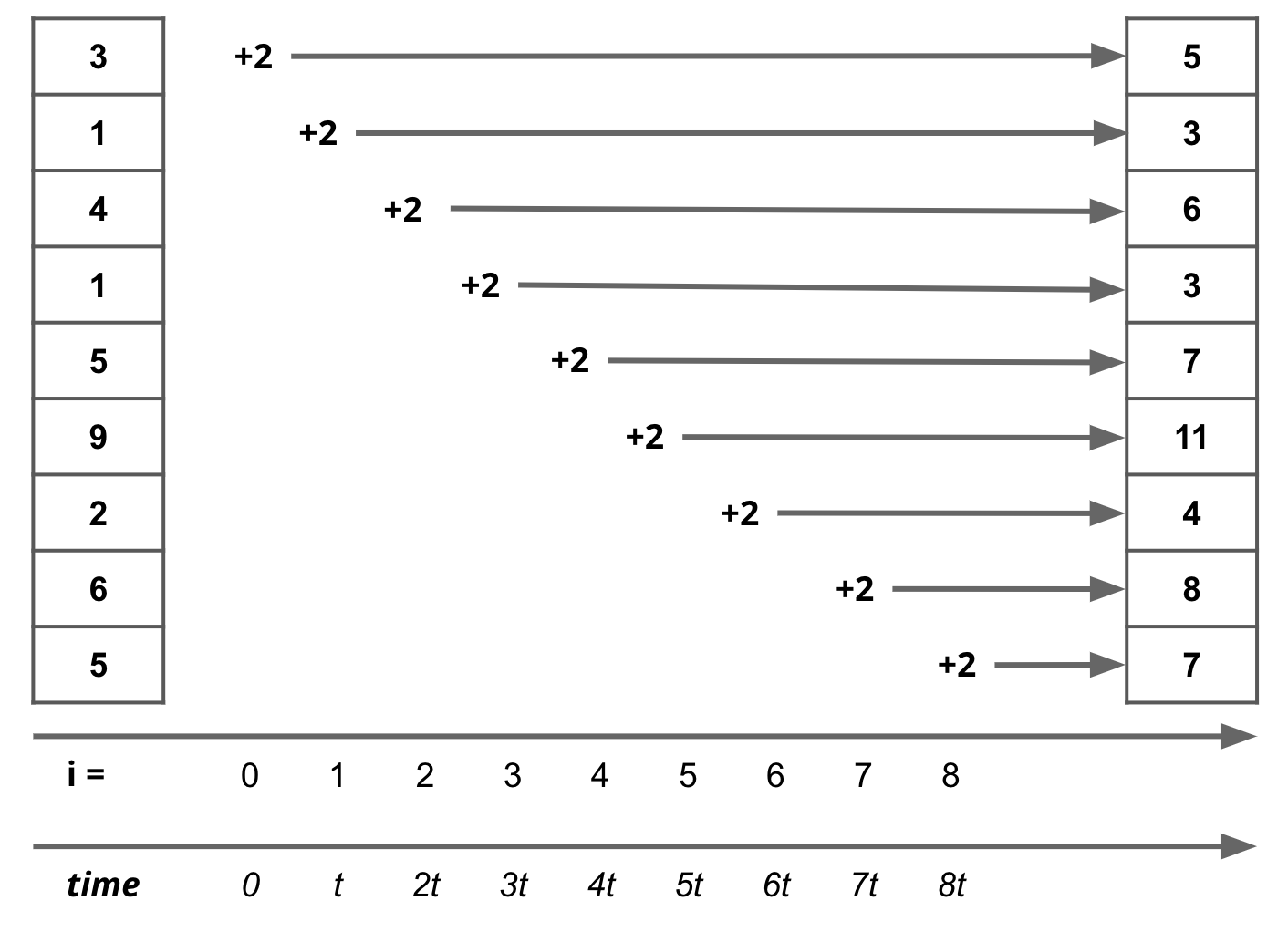
Fig. 1.3 If an iteration takes time t, then the total time taken by the algorithm is n*t where n is length of data

This is a good theoretical framework because it measures how the algorithm’s speed independent of hardware considerations.

Space Complexity

I don’t have a lot to say on the issue of space or memory consumption but it is critical.

Improving speed of an algorithm often comes at the cost of more memory consumption. That is, improving speed of an algorithm often necessitates creation or use of data structures that allow faster data retrieval and processing times. In that sense, speed and memory have an inherent tension in Computer Science. In this course, we are going to use such data structures that are going to result in very fast code. But the price we have to pay as a result is that we can only work with data sets that can fit within our memory. For most people it is going to be on the order of 8-16 GB.

Datasets of today are often much larger than this and require alternative paradigms of computer programming such as Distributed Computing, Parallel Programming, Concurrent Programming etc.

Vectorization

Vectorization is the process of applying operations to entire arrays at once, rather than their individual elements sequentially. Vectorization is also called Array Programming. It is usually much faster than using loops.

In this course, we will be minimizing the use of loops.

1. Serial / Sequential Operations	2. Vectorized Operations

Vectorization can only be applied in situations when operations at individual elements are independent of each other. For example, if we want to add two arrays, we can do so by adding each element of the first array to the corresponding element of the second array. This is a vectorized operation.

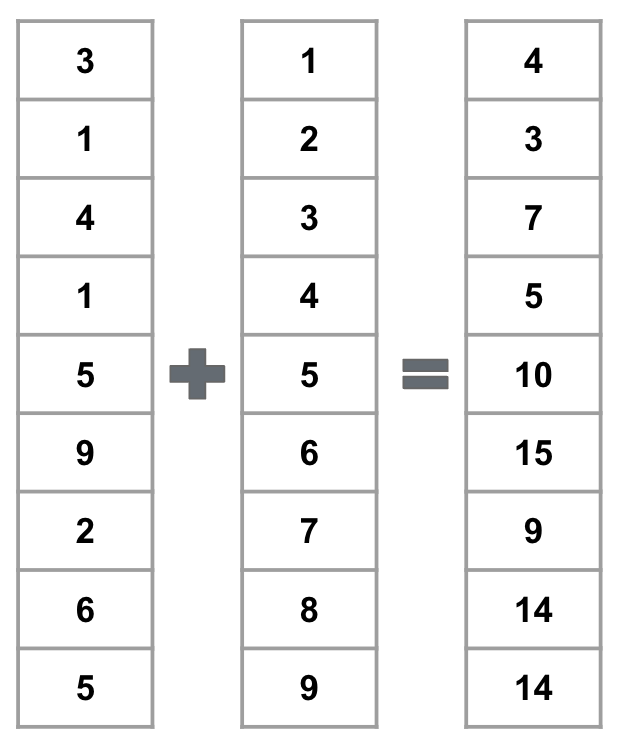
Fig. 1.4 Adding two arrays

However, for problems such as the Fibonacci sequence, where the value of an element depends on the values of the previous two elements, we cannot vectorize the operation. Similarly, finding minimum or maximum of an array cannot be vectorized.

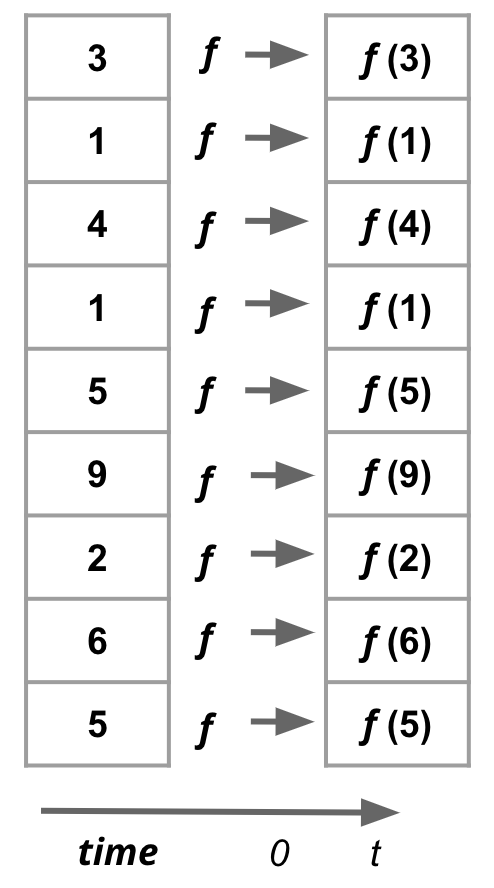
Fig. 1.5 Vectorized operations, more generally, can be application of any function f to each element of an array.

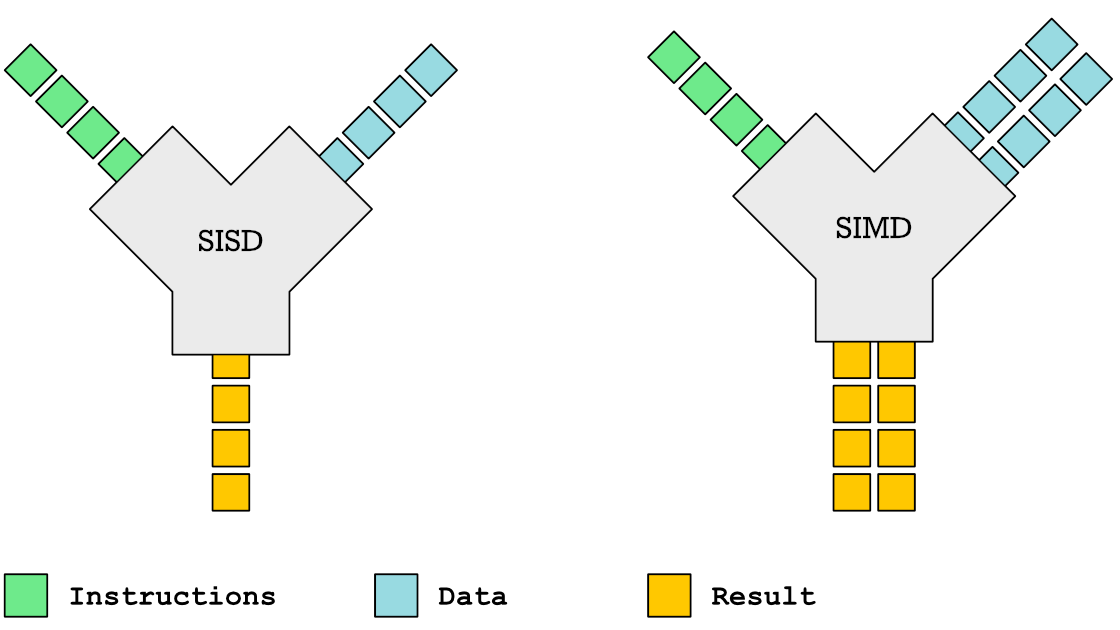
Fig. 1.6 Vectorized operations are also known as SIMD (Single Instruction Multiple Data) operations in the context of computer architecture. In contrast, scalar operations are known as SISD (Single Instruction Single Data) operations.

Filtering certain entries in a vectorized array is also very easy using boolean indexing or boolean maps of the same length. Elements corresponding to True values are kept, while elements corresponding to False values are discarded.

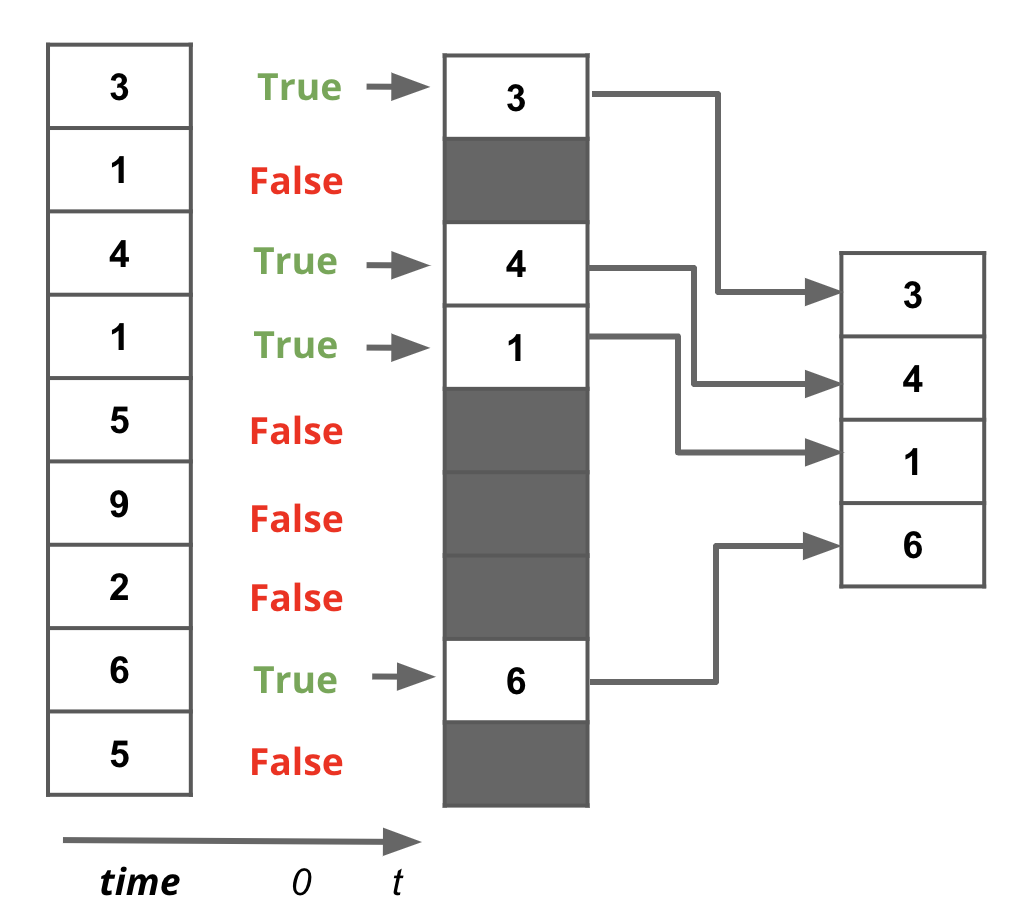
Fig. 1.7 Filtering a vectorized array using a boolean map

pandas and pretty much all modern data science and AI libraries heavily rely on Vectorized operations to process and operate on large datasets.