5.5. Tree Recursion

Another common pattern of computation is called tree recursion.

Tree recursion is different from linear recursion in that there are >1 recursive calls that the function makes to itself.

5.5.1. Negative Example: Fibonacci Numbers

As an example, consider computing the sequence of Fibonacci numbers, in which each number is the sum of the preceding two:

\[ 0,1,1,2,3,5,8,13,21,... \]

In general, the Fibonacci numbers can be defined by the rule

\[\begin{split} \text{Fib}(n) = \begin{cases} 0 & \text{if } n = 0 \\ 1 & \text{if } n = 1 \\ \text{Fib}(n-1) + \text{Fib}(n-2) & \text{otherwise} \end{cases} \end{split}\]

We can immediately translate this definition into a recursive function for computing Fibonacci numbers:

def fib(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fib(n-1) + fib(n-2)
    
fib(5)

5

Consider the pattern of this computation.

To compute fib(5), we compute fib(4) and fib(3).

To compute fib(4), we compute fib(3) and fib(2) and so on.

In general, the evolved process looks like a tree, as shown in the figure below. Notice that the branches split into two at each level (except at the bottom); this reflects the fact that the fib function calls itself twice each time it is invoked.

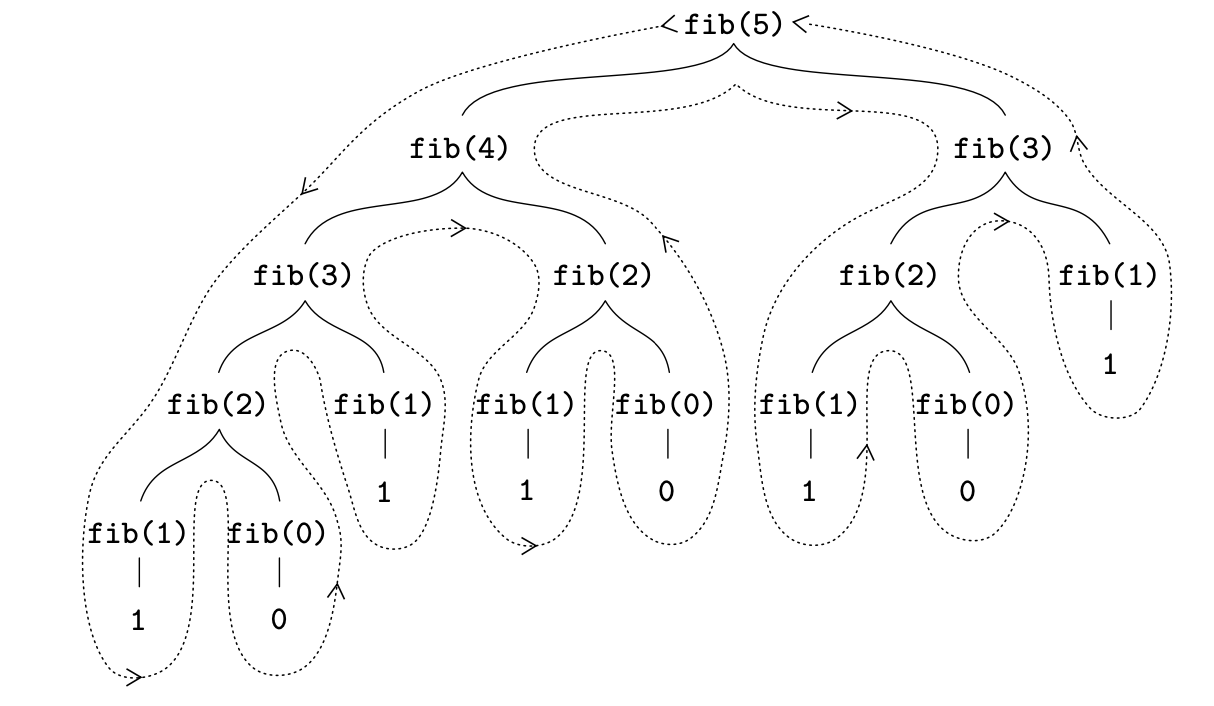
Fig. 5.6 The tree-recursive process generated in computing fib(5).

5.5.1.1. Time and Space Complexity

This function is instructive as a prototypical tree recursion, but it is a terrible way to compute Fibonacci numbers because it does so much redundant computation.

Notice in figure above that the entire computation of fib(3)— almost half the work—is duplicated.

In fact, it is not hard to show that the number of times the function will compute fib(1) or fib(0) (the number of leaves in the above tree, in general) is precisely \(\text{Fib}(n + 1)\). To get an idea of how bad this is, one can show that the value of \(\text{Fib}(n)\) grows exponentially with \(n\).

Thus, the process uses a number of steps that grows exponentially with the input.

On the other hand, the space required grows only linearly with the input, because we need keep track only of which nodes are above us in the tree at any point in the computation.

In general, the number of steps required by a tree-recursive process will be proportional to the number of nodes in the tree, while the space required will be proportional to the maximum depth of the tree.

5.5.1.2. Iterative Version

We can also formulate an iterative process for computing the Fibonacci numbers. The idea is to use a pair of integers a and b, initialized to \(\text{Fib}(1) = 1\) and \(\text{Fib}(0) = 0\), and to repeatedly apply the simultaneous transformations

\[ a \leftarrow a + b \]

\[ b \leftarrow a \]

It is not hard to show that, after applying this transformation n times, a and b will be equal, respectively, to \(\text{Fib}(n + 1)\) and \(\text{Fib}(n)\). Thus, we can compute Fibonacci numbers iteratively using the function

def fib_iter(n):
    a, b = 0, 1
    for i in range(n):
        a, b = b, a+b
    return a

fib_iter(15)

610

This second method for computing Fib(n) is linear iteration. The difference in number of steps required by the two methods—one linear in \(n\), one growing as fast as \(\text{Fib}(n)\) itself—is enormous, even for small inputs.

5.5.1.3. Avoiding Tree Recursion

One should not conclude from this that tree-recursive processes are useless.

When we consider processes that operate on hierarchically structured data rather than numbers, we will find that tree recursion is a natural and powerful tool. But even in numerical operations, tree-recursive processes can be useful in helping us to understand and design programs.

For instance, although the recursive fib function is much less efficient than the iterative one, it is more straightforward, being little more than a translation into code of the mathematical definition of the Fibonacci sequence.

To formulate the iterative algorithm required noticing that the computation could be recast as an iteration with three state variables.

5.5.2. Positive Example: Merge Sort

Another example of a tree-recursive process is merge sort.

The idea behind merge sort is to divide the array into two halves, sort each of the halves, and then merge the sorted halves to produce a sorted whole.

Fig. 5.7 Animation of the merge sort algorithm.

The merge sort algorithm can be described as follows:

1. If the array has 0 or 1 element, it is already sorted, so return.

2. Otherwise, divide the array into two halves.

3. Sort each half.

4. Merge the two halves.

The merge function is a helper function that merges two sorted arrays into a single sorted array.

Fig. 5.8 The merge function merges two sorted arrays into a single sorted array and is central to the merge sort algorithm.

def merge(left, right):
    result = []
    i, j = 0, 0
    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1
    result += left[i:]
    result += right[j:]
    return result

5.5.2.1. Recursive Implementation

The merge sort algorithm can be implemented using a recursive function, as shown below.

def merge_sort(arr):
    if len(arr) <= 1:
        # base case
        return arr
    else:
        mid = len(arr) // 2
        left = merge_sort(arr[:mid])
        right = merge_sort(arr[mid:])
        return merge(left, right)

The figure below shows the tree-recursive process generated in sorting the array [5, 3, 8, 6, 2, 7, 1, 4] using the merge sort algorithm.

Fig. 5.9 The tree-recursive process generated in sorting the array [5, 3, 8, 6, 2, 7, 1, 4] using the merge sort algorithm.

Note that the recursive implementation of merge sort is still divide and conquer as it divides the array into two halves and conquers by sorting each half.

5.5.2.2. Iterative Implementation

Contrast the elegant simplicity of the tree-recursive merge sort with the iterative process of the selection sort algorithm, which is a simple sorting algorithm that works by repeatedly selecting the minimum element from the unsorted portion of the array and moving it to the beginning of the unsorted portion.

def merge_sort_iterative(data):
  result = []

  for x in data:
    result.append([x])

  while len(result) > 1:
    newlist = []
    i = 0
    while i <= len(result) - 1:
      if i+1 == len(result): 
        newlist.append(result[i])
      else:
        list1 = result[i]
        list2 = result[i+1]
        merged = merge(list1, list2)
        newlist.append(merged)
      i = i + 2

    result = newlist

  return result[0]

5.5.2.3. Time and Space Complexity

The space and time complexity of merge sort algorithm remains unchanged whether it is implemented using a recursive or iterative processes.

The time complexity of the merge sort algorithm is \(O(n \log n)\), where \(n\) is the number of elements in the array.

The space complexity of the merge sort algorithm is \(O(n)\), where \(n\) is the number of elements in the array.

5.5.3. Quick Sort

Recall from Section 4.3. that Quick Sort is a sorting algorithm that uses a divide and conquer strategy. It works by selecting a pivot element from the array and partitioning the other elements into two sub-arrays according to whether they are less than or greater than the pivot. The sub-arrays are then sorted recursively.

This can be done in-place, requiring a constant amount of extra memory and allowing the algorithm to be run in-place. In other words, the space complexity of Quick Sort is O(1) compared to O(n) for Merge Sort.

5.5.3.1. Algorithm

The steps are:

1. Pick an element from the list and call it pivot. This is typically the last element in the list.

2. Partitioning: reorder the list so that all elements with values less than the pivot come before the pivot, while all elements with values greater than the pivot come after it (equal values can go either way). After this partitioning, the pivot is in its final position. This is called the partition operation.

3. Recursively apply the above steps to two sub-lists: one to the left of pivot with elements that all have smaller values and separately to sub-list on the right of pivot containing elements with greater values.

The base case of the recursion are arrays of size zero or one, which are in order by definition, so they never need to be sorted.

The pivot selection and partitioning steps can be done in several different ways; the choice of specific implementation schemes greatly affects the algorithm’s performance.

5.5.3.2. Implementation

The partitioning step, as described in the algorithm, is the most important part of the Quick Sort algorithm. The partitioning step is implemented using the following steps:

1. Initialize pivot to the last element of the array.

2. Initialize left to start of the array and right to the second last element of the array.

3. As the goal is to move all elements less than pivot to the left and all elements greater than pivot to the right, we need to do the following: 3.1. Until the element at left is less than pivot, increment left 3.2. Until the element at right is greater than pivot, decrement right 3.3. If element at left is less than element at right, swap them. 3.4. Continue until left is greater than right.

def partition(data, start, end):

    pivot = data[end]
    left = start
    right = end - 1

    while left < right:

        # move left towards right
        while data[left] < pivot:
            left = left + 1

        # move right towards left
        while right > 0 and data[right] > pivot:
            right = right - 1

        if left < right:
            data[left], data[right] = data[right], data[left]
	
    # insert pivot into its correct place
    data[left], data[end] = data[end], data[left]

    return left

Once we have the partititon function, the Quick Sort algorithm itself is fairly simple.

The basic idea idea is to call partition on data which returns the new location of pivot.

Using the new location of pivot, we recursively call quicksort on the sublists to the left and right of the pivot.

def quicksort(data, low, high):
    if low < high:
        pi = partition(data, low, high)
        quicksort(data, low, pi-1)
        quicksort(data, pi+1, high)

Fig. 5.10 Quicksort diagram. Cells with dark backgrounds represent pivot.
Red boxes correspond to pi = partition(arr, low, high).
Yellow boxes correspond to the first recursive call: quicksort(arr, low, pi-1).
Orange boxes correspond to the second recursive call: quicksort(arr, pi+1, high).

5.5.3.3. Complexity

As discussed before, the space complexity of Quick Sort is O(1) compared to O(n) for Merge Sort since no extra space is required that is dependent on the size of the input.

The worst case time complexity of quick sort is \(O(n^2)\) and the average case time complexity is O(n log n). This is because the worst case occurs when the pivot is the smallest or largest element in the array.

If the pivot is the smallest or largest element, then the partitioning step will only move one element to the left or right of the pivot. This means that the partitioning step will take O(n) time and we will have to do this for every element in the array.

5.5.4. Tower of Hanoi

Tower of Hanoi is a mathematical puzzle where we have three towers (aka rods and pegs) and n disks.

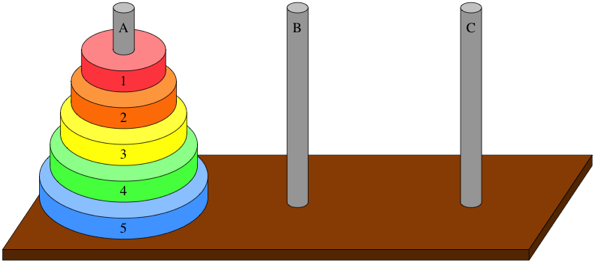
Fig. 5.11 Tower of Hanoi with towers labeled A, B, and C from left to right. There are 5 disks labeled 1 through 5 from top to bottom.

The goal of the puzzle is to move the entire stack of disks from tower A to tower C, obeying the following three simple rules:

1. Only one disk can be moved at a time.

2. A disk can only be moved if it is the uppermost disk on a stack.

3. No disk may be placed on top of a smaller disk.

Fig. 5.12 Optimal solution to Tower of Hanoi problem with 4 disks. The number of steps required to solve a Tower of Hanoi puzzle is \(2^n - 1\), where n is the number of disks.

The puzzle can be played with any number of disks, although many toy versions have around 7 to 9 of them. The minimum number of moves required to solve a Tower of Hanoi puzzle is \(2^n - 1\), where n is the number of disks.

5.5.4.1. Implementation

The Tower of Hanoi is a naturally recursive problem.

The recursive solution is based on the observation that to move n disks from tower A to tower C:

Step 1. We can move n-1 disks from tower A to tower B

Step 2. Then move the nth disk from tower A to tower C

Step 3. Finally move n-1 disks from tower B to tower C.

In python, these recursive steps can be implemented as follows:

def hanoi(n, source="A", buffer="B", destination="C", disk=1):
    """
    Move n disks from source to destination, using buffer, as needed
    """
    
    if n == 1:
        
        print("Move disk", disk, "from", source, "to", destination)

    else:
        
        hanoi(n-1, source="A", buffer="C", destination="B")            # step 1
        hanoi(1,   source="A", buffer="B", destination="C", disk=n)    # step 2
        hanoi(n-1, source="B", buffer="A", destination="C")            # step 3
    
hanoi(3)

Move disk 1 from A to B
Move disk 2 from A to C
Move disk 1 from B to C
Move disk 3 from A to C
Move disk 1 from A to B
Move disk 2 from A to C
Move disk 1 from B to C

The base case of the recursion is when there is only one disk to move. In this case, we simply move the disk from the source tower to the destination tower.

5.5.4.2. Complexity

The time complexity of the Tower of Hanoi is \(O(2^n)\) and the space complexity is O(n).

The time complexity is exponential because the number of moves required to solve the puzzle is \(2^n - 1\), where n is the number of disks.

5.5.4.3. Legend

Accompanying the game was an instruction booklet, describing the game’s purported origins in Tonkin, and claiming that according to legend Brahmins at a temple in Benares have been carrying out the movement of the “Sacred Tower of Brahma”, consisting of 64 golden disks, according to the same rules as in the game, and that the completion of the tower would lead to the end of the world!

If the legend were true, and if the priests were able to move disks at a rate of one per second, using the smallest number of moves, it would take them \(2^{64} − 1\) seconds or roughly 585 billion years to finish, which is about 42 times the estimated current age of the universe 😅.