7.1. Stacks#

A stack is a collection of objects set on top of each other.
Note that this organization imposes constraints on the order in which objects can be added or removed. That is, the last object placed on the stack is the first one to be removed. This is known as the Last-In-First-Out (LIFO) order.
Stacks are integral to computer science. They are used to store and manage function calls, to implement certain types of algorithms, and to manage memory.
7.1.1. Operations#
Stacks, in essence, are defined by the operations they support. These operations are:
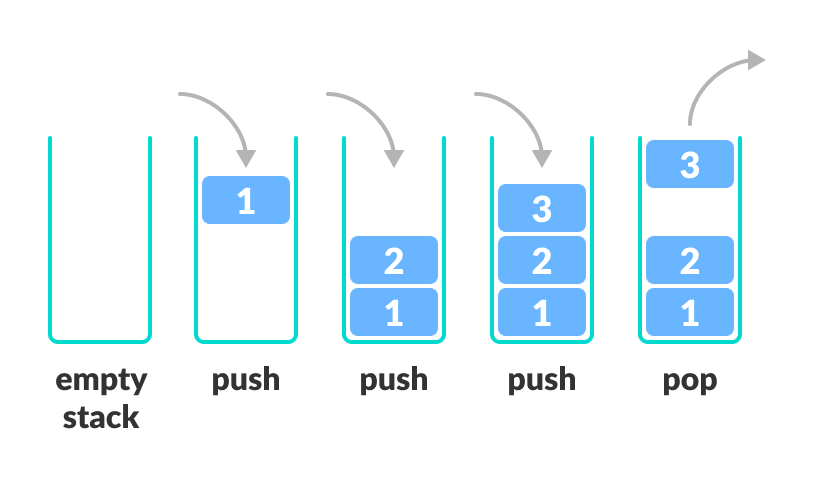
Push: Adds a given element to the top of the stack.
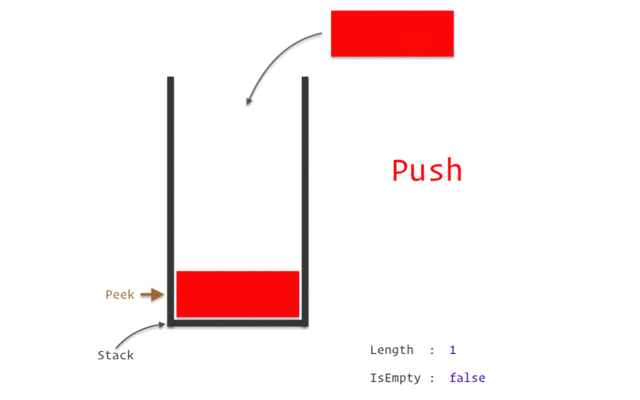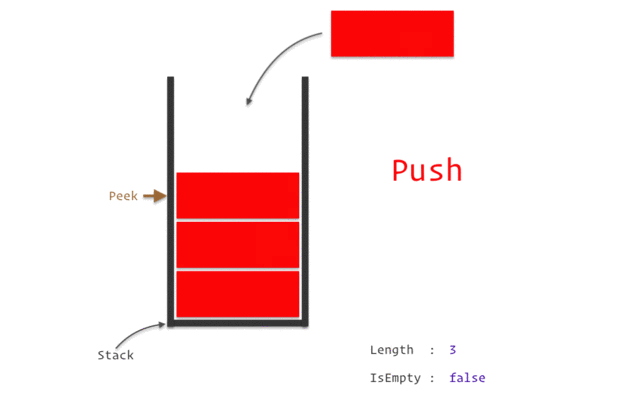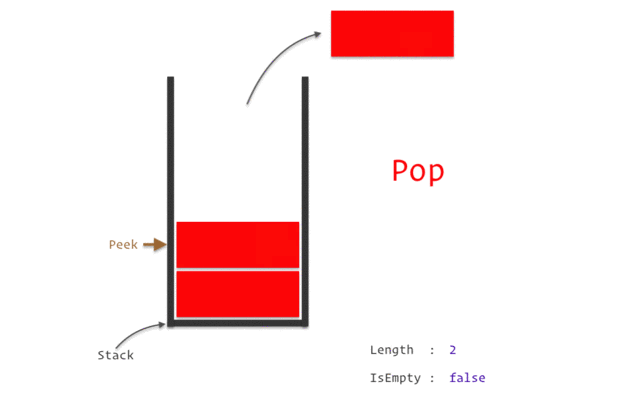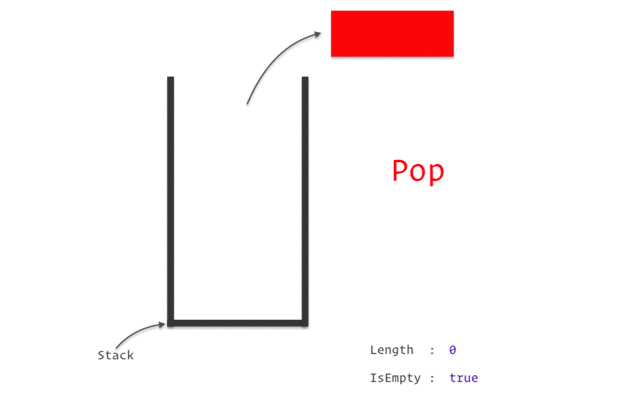
Pop: Removes the top element from the stack.
Empty: Returns
Trueif the stack is empty,Falseotherwise.
Peek: Returns the top element of the stack, without removing it.
This operation is also known astoporfrontorhead.
Size: Returns the number of elements in the stack.
This operation is also known aslengthorcount.
Equally important to the operations that a stack supports is the operations that it does not support.
In other words, stacks do not support:
❌ Reading, inserting and removing elements from/at arbitrary positions.
✅ You can access, insert or remove the element at the top of the stack only.
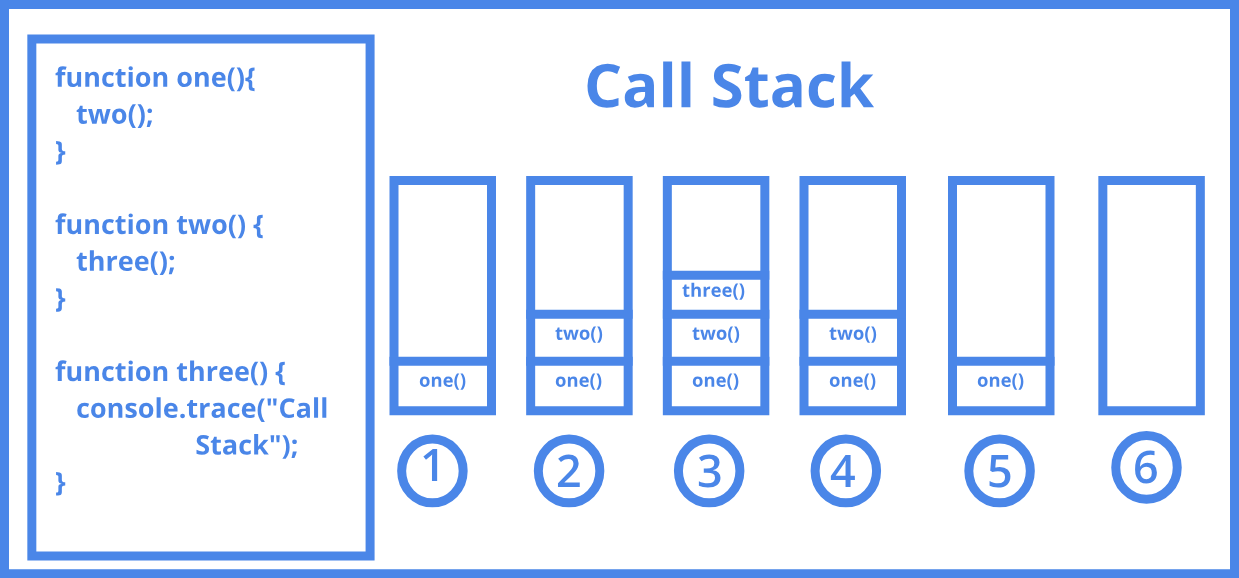
7.1.2. Application 1: Call Stacks#
A Call Stack is a stack data structure that keeps track of and manages active function (or subroutine or method or procedure) in a computer program at any given time.
This kind of stack is also known as an “execution stack”, “control stack”, “run-time stack”, or “machine stack”, and is often shortened to just “the stack”.
The call stack is used for several related purposes, but the main reason for having a call stack is to keep track of the point to which each active function should jump to when it finishes executing.
7.1.2.1. Stack Frame#
A Stack Frame is a data structure that contains information about the state of a function (or subroutine or method or procedure).
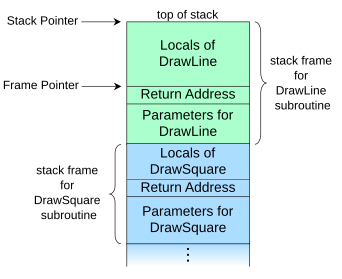
When a function is called, a new frame is pushed onto the stack. This frame contains information about the function, such as its arguments and local variables.
When a function returns, the frame is popped off the stack. This allows the program to return to the point where the function was called.
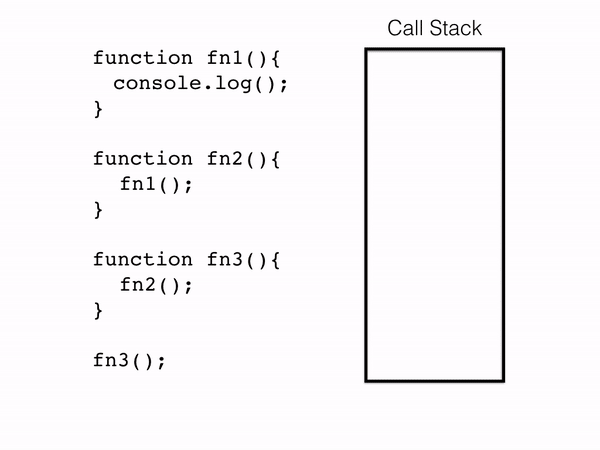
7.1.2.2. Stack Trace#
Stack trace (also known as stack back track or stack trace back) is a list of the function calls, and their corresponding stack frames, at some point in the execution of a program.
Any time a program crashes, most programming languages will print a stack trace to the console. This is a list of all the functions that were called up to the point of the crash, and it is a very useful tool for debugging. By examining the stack trace, you can determine the sequence of function calls that led to the crash.
As an example, the following Python program contains an error.
def a():
i = 0
j = b(i) # line 3
return j
def b(z):
k = 5
if z == 0:
c() # line 9
return k + z
def c():
error() # line 13
a() # line 15
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Input In [1], in <cell line: 15>()
12 def c():
13 error() # line 13
---> 15 a()
Input In [1], in a()
1 def a():
2 i = 0
----> 3 j = b(i) # line 3
4 return j
Input In [1], in b(z)
7 k = 5
8 if z == 0:
----> 9 c() # line 9
10 return k + z
Input In [1], in c()
12 def c():
---> 13 error()
NameError: name 'error' is not defined
7.1.2.3. Stack Overflow#
Stack overflow is a common problem in recursive programs. It occurs when the stack is full and there is no more space to push new function calls.
This can happen if a recursive function calls itself too many times, or if the function has a large number of local variables. When a stack overflow occurs, the program will crash with a “stack overflow” error.
def f():
f()
f()
---------------------------------------------------------------------------
RecursionError Traceback (most recent call last)
Cell In[3], line 4
1 def f():
2 f()
----> 4 f()
Cell In[3], line 2, in f()
1 def f():
----> 2 f()
Cell In[3], line 2, in f()
1 def f():
----> 2 f()
[... skipping similar frames: f at line 2 (2970 times)]
Cell In[3], line 2, in f()
1 def f():
----> 2 f()
RecursionError: maximum recursion depth exceeded
7.1.3. Application 2: Undo and History#
Stacks are also used to implement undo functionality in many applications.
For example, when you type text into a text editor, the editor keeps track of the changes you make. If you make a mistake, you can undo the changes by pressing Ctrl+Z.
The editor does this by storing the changes in a stack. When you press Ctrl+Z, the editor pops the last change off the stack and applies it to the text.
This is a simple example of how stacks can be used to implement undo functionality. Stacks can also be used to implement history functionality, where you can navigate through the changes you have made to a document.

Similarly, stacks can be used to implement the forward and back buttons in a web browser. When you click on a link, the browser pushes the current page onto a stack and loads the new page. If you click the back button, the browser pops the last page off the stack and loads it.
7.1.4. Application 3: Parsing#
Stacks are also used in parsing and expression evaluation.
For example, when you write a program in a programming language, the compiler or interpreter uses a stack to keep track of the order of operations in the program.
Similarly, when you evaluate an expression, such as 3 + 4 * 5, the computer uses a stack to keep track of the order of operations.
Some problems that can be solved using stacks are:
Balanced Parentheses: Check if a given expression has balanced parentheses. For example,
((()))is balanced, while(()))is not.Infix to Postfix: Convert an infix expression to a postfix expression. For example, convert
3 + 4 * 5to3 4 5 * +.Evaluate Postfix: Evaluate a postfix expression. For example, evaluate
3 4 5 * +to23.
7.1.5. Implementation#
class Stack:
def __init__(self):
self.__data = []
def push(self, value):
self.__data.append(value)
def pop(self):
return self.__data.pop()
def peek(self):
return self.__data[-1]
def is_empty(self):
return len(self.__data) == 0
def __str__(self):
return str(self.__data)
def __len__(self):
return len(self.__data)
s = Stack()
assert s.is_empty() == True, "Test case 1 failed"
s.push(1)
s.push(2)
assert s.is_empty() == False, "Test case 2 failed"
assert s.pop() == 2, "Test case 3 failed"
assert s.peek() == 1, "Test case 4 failed"
assert s.pop() == 1, "Test case 5 failed"
assert s.is_empty() == True, "Test case 6 failed"
print("All test cases passed")
All test cases passed
7.1.6. Space and Time Complexity#
The space complexity of a stack is O(n), where n is the number of elements in the stack. This is because the stack stores each element in a separate node.
The time complexity of the push, pop, peek, empty, and size operations is O(1). This is because these operations only involve updating the top of the stack, which can be done in constant time.
