2.1. Linear Search

Linear Search (also known as Sequential Search) is a brute force search algorithm that finds a target value within a list by sequentially checking each element of the list until a match is found.

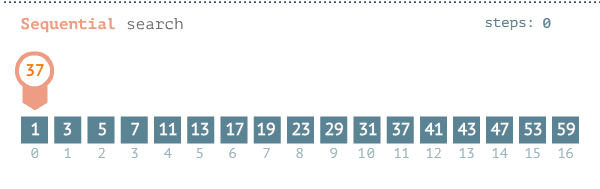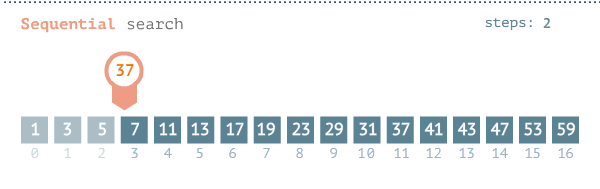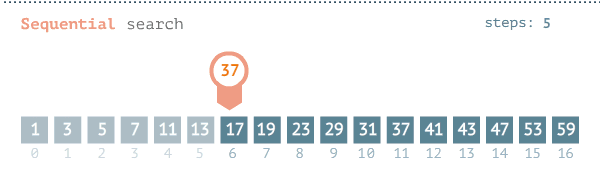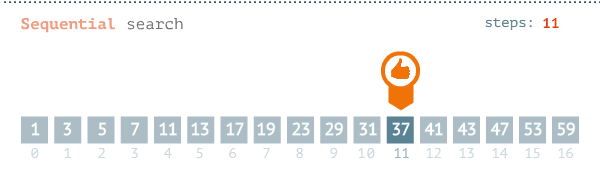
The pseudocode for the algorithm is as follows:

Algorithm 2.1 (Linear Search Algorithm)

Inputs Given a list of numbers \(L\) of length \(n\) and a target value \(t\)

Output The index of the target value \(t\) in the list \(L\) of length \(n\)

1. For \(i\) from \(0\) to \(n-1\):

   1.1. If \(L[i] == t\):
   1.1.1. Return \(i\)
   1.2. end If

2. end For

3. Return -1

Python implementation of the algorithm is as follows:

data = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
query = 5

def linear_search(data, query):
    """
    Returns the index position of the target if found, else returns -1
    """
    i = 0
    while i < len(data):
        if data[i] == query:
            return i
    return -1

linear_search(data, query)

2.1.1. Analysis

The time complexity of the above algorithm is O(n) since in the worst case we have to iterate over the entire list to find the target.

In best case, the target is found at the first index, thus the best case is O(1).

Assuming uniform distribution of the target value, the average case is If each element is equally likely to be searched, then linear search has an average case of \( \frac{n+1}{2}\) comparisons. Thus, the average case is O(n).

The space complexity of the above algorithm is O(1) since we are not using any extra space.