8.2. Doubly Linked Lists

Doubly linked lists are a type of linked list where each node contains two references:

1. a reference to the next node, same as singly linked lists

2. a pointer to the previous node (🆕!)

This allows for more efficient traversal of the list in both directions.

Fig. 8.12 A doubly linked list is a type of linked list where each node contains a pointer to the next node and a pointer to the previous node.

The small disadvantage of doubly linked lists is that they require more memory than singly linked lists because each node contains an extra pointer.

8.2.1. Node class

To implement a doubly linked list, we need to define a Node class that contains a data attribute and next and prev pointers.

Fig. 8.13 Node in a doubly linked list has a reference to the next and previous node

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None
        self.prev = None

8.2.2. DoublyLinkedList class

We also need to define a DoublyLinkedList class that contains a head pointer (reference), and optionally a tail pointer (reference).

class DoublyLinkedList:
    def __init__(self):
        self.head = None
        self.tail = None

Note that the initialization of a doubly linked list is exactly the same as that of a singly linked list.

8.2.3. Traversal

To traverse a doubly linked list, we can start at the head node and move to the next node until we reach the end of the list (all the same as singly linked lists).

def traverse(self):
    current = self.head
    while current:
        print(current.data)
        current = current.next

To traverse a doubly linked list in reverse (🆕🆕🆕), we can start at the tail node and move to the previous node until we reach the beginning of the list.

def reverse_traverse(self):
    current = self.tail
    while current:
        print(current.data)
        current = current.prev

Note that at any given time, the beginning and end of a doubly linked list are delimited by the following:

• Beginning: the head node’s prev pointer is None

• End: the tail node’s next pointer is None

8.2.4. Insertion

Similar to singly linked lists, the steps required for insertion are different based on the position of the new node.

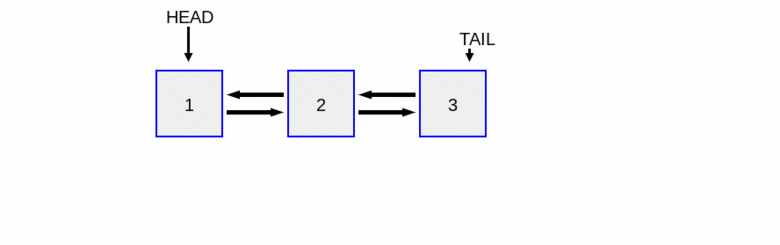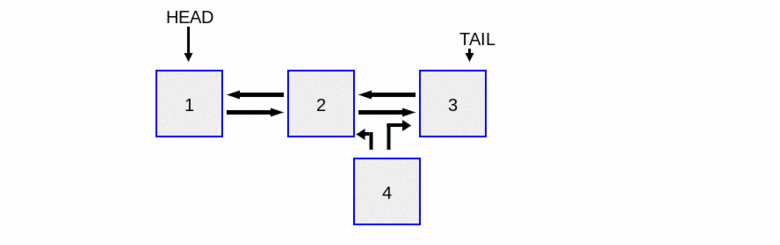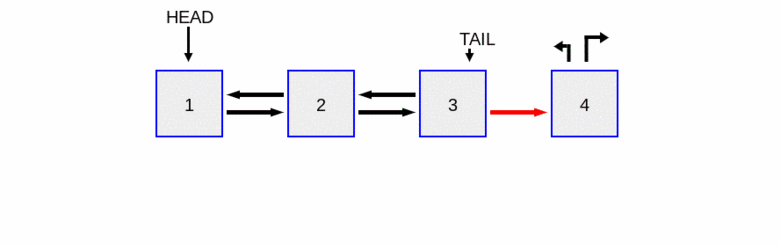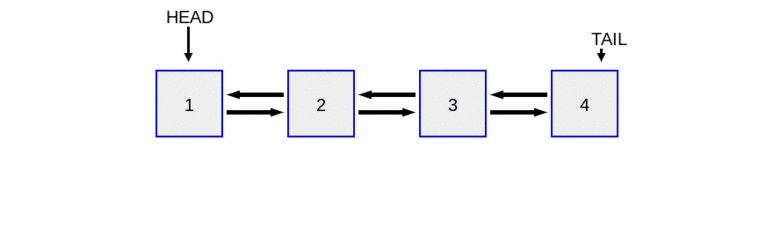
To insert a new node at the beginning of a doubly linked list, we need to:

1. update the prev pointer of the current head node to now point to the new_node.

2. update the next pointer of the new node to point to the current head node.

3. update the head pointer to point to the new_node.

def insert_at_beginning(self, data):
    new_node = Node(data)
    if not self.head:
        self.head = new_node
        self.tail = new_node
    else:
        new_node.next = self.head
        self.head.prev = new_node
        self.head = new_node

To insert a new node at the end of a doubly linked list, we need to:

1. update the next pointer of the current tail node to point to the new_node.

2. update the prev pointer of the new node to point to the current tail node.

3. update the tail pointer to point to the new_node.

def insert_at_end(self, data):
    new_node = Node(data)
    if not self.head:
        self.head = new_node
        self.tail = new_node
    else:
        new_node.prev = self.tail
        self.tail.next = new_node
        self.tail = new_node

To insert a new node at a given position in a doubly linked list, we need to:

1. update the next pointer of the previous node to point to the new node.

2. update the prev pointer of the next node to point to the new node.

3. update the prev and next pointers of the new node to point to the previous and next nodes, respectively.

def insert_at_position(self, data, position):
    if position < 0:
        print("Invalid position")
        return
    if position == 0:
        self.insert_at_beginning(data)
    else:
        new_node = Node(data)
        current = self.head
        for _ in range(position - 1):
            if not current:
                print("Invalid position")
                return
            current = current.next
        new_node.next = current.next
        new_node.prev = current
        if current.next:
            current.next.prev = new_node
        current.next = new_node

8.2.5. Deletion

To delete a node at the beginning of a doubly linked list, we need to update the prev pointer of the next node and the head pointer.

def delete_at_beginning(self):
    if not self.head:
        print("List is empty")
    elif self.head == self.tail:
        self.head = None
        self.tail = None
    else:
        self.head = self.head.next
        self.head.prev = None

To delete a node at the end of a doubly linked list, we need to update the next pointer of the previous node and the tail pointer.

def delete_at_end(self):
    if not self.head:
        print("List is empty")
    elif self.head == self.tail:
        self.head = None
        self.tail = None
    else:
        self.tail = self.tail.prev
        self.tail.next = None

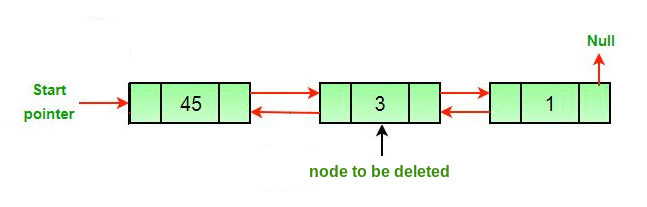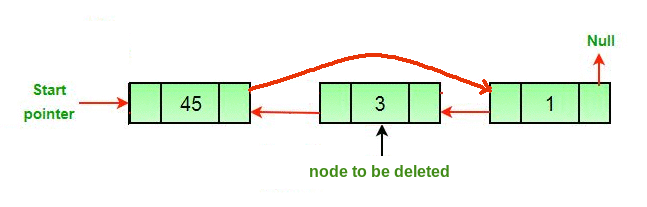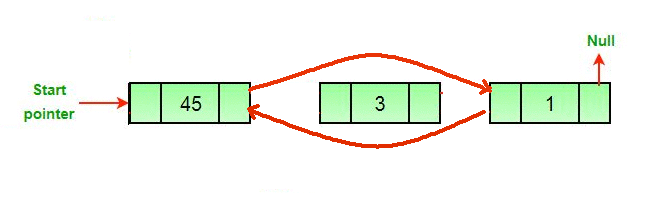
To delete a node at a given position in a doubly linked list, we need to update the next pointer of the previous node, the prev pointer of the next node, and the prev and next pointers of the node to be deleted.

def delete_at_position(self, position):
    if position < 0:
        print("Invalid position")
        return
    if position == 0:
        self.delete_at_beginning()
    else:
        current = self.head
        for _ in range(position):
            if not current:
                print("Invalid position")
                return
            current = current.next
        if current == self.tail:
            self.delete_at_end()
        else:
            current.prev.next = current.next
            current.next.prev = current.prev

8.2.6. Analysis

The time complexity of inserting a node at the beginning or end of a doubly linked list is O(1) because we only need to update the prev and next pointers of a few nodes.

The time complexity of inserting a node at a given position in a doubly linked list is O(n) because we may need to traverse the list to find the previous node.

The time complexity of deleting a node at the beginning or end of a doubly linked list is O(1) because we only need to update the prev and next pointers of a few nodes.

The time complexity of deleting a node at a given position in a doubly linked list is O(n) because we may need to traverse the list to find the node to be deleted.