3.1. Selection Sort

Selection sort is a simple decrease and conquer sorting algorithm that works by maintaining two sublists in a given array:

1. The sublist which is already sorted.

2. Remaining sublist which is unsorted.

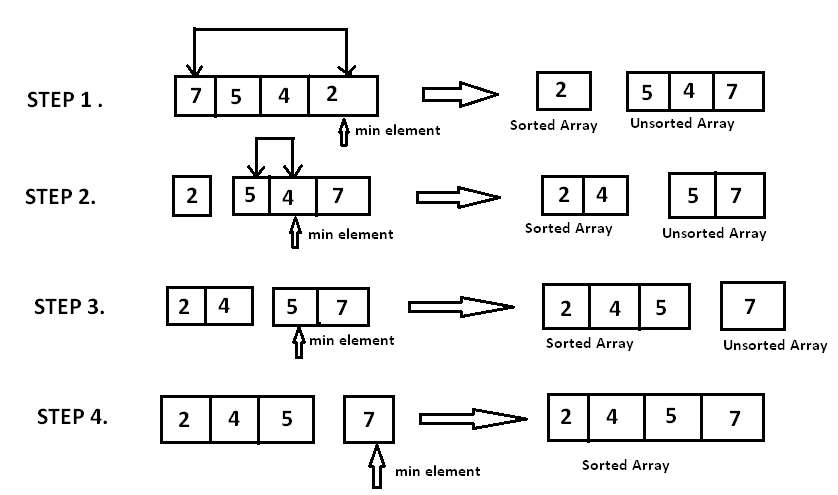
The algorithm iteratively “selects” the smallest (for ascending order) element from the unsorted sublist and appends it to the end of the sorted sublist. This process continues until the unsorted sublist is empty.

Note that the algorithm does not require any extra space and is thus an in-place sorting algorithm. The two sublists are maintained by a single variables tracking the first element of the unsorted sublist. Everything before this variable is sorted and everything after it is unsorted.

Fig. 3.3 Selection Sort iteratively selects the smallest element from the unsorted sublist and appends it to the end of the sorted sublist.

Selection sort “conquers” the sorting problem by “decreasing” the size of the unsorted sublist by one in each iteration.

3.1.1. Algorithm

The selection sort algorithm, conceptually in broad steps, works as follows:

1. Initialize a iterator \(i\) to \(0\).

2. Identify the smallest element in the unsorted sublist (from \(i\) to \(n-1\)).

3. Swap the smallest element with the element at index \(i\).

4. Increment \(i\) by \(1\).

5. Repeat steps 2-4 until \(i\) is equal to \(n-1\).

3.1.2. Psuedocode

Algorithm 3.1 (Selection Sort Algorithm)

Inputs Given a list of numbers \(L\) of length \(n\)

Output A sorted list of numbers \(L\) of length \(n\)

For \(i\) from \(0\) to \(n-1\):
  \(min\) \(\leftarrow\) \(i\)
  For \(j\) from \(i+1\) to \(n-1\):
    If \(L[min] > L[j]\):
      \(min\) \(\leftarrow\) \(j\)
    end If
  end For
  Swap \(L[i]\) and \(L[min]\)
end For

3.1.3. Analysis

Time Complexity of selection sort is \(O(n^2)\) in all cases.

In the worst case, the list is sorted in reverse order. In this case, the algorithm will perform \(n\) comparisons and \(n\) swaps. Thus, the time complexity is \(O(n^2)\).

In the best case, the list is already sorted. In this case, the algorithm still performs \(n^2\) comparisons but does \(0\) swaps. Thus, the time complexity is \(O(n^2)\).

In the average case, the list is not sorted. In this case, the algorithm will perform \(n\) comparisons and \(n/2\) swaps. Thus, the time complexity is \(O(n^2)\).

Space Complexity of selection sort is \(O(1)\). This is because the algorithm sorts the list in-place.