2. Brute Force#

Brute Force Algorithms are exactly what they sound like – straightforward methods that relying on sheer computing power to try every possibility rather than using insight to efficiently narrow down the possibilities. Brute force algorithms are also known as “exhaustive search” algorithms, because they try all possible answers until they find the right one.
For example, imagine you have a small padlock with 4 digits, each from 0-9. You forgot your combination, but you don’t want to buy another padlock. Since you can’t remember any of the digits, you have to use a brute force method to open the lock. So you set all the numbers back to 0 and try them one by one: 0001, 0002, 0003, and so on until it opens. In the worst case scenario, it will take you 10,000 tries to open the lock.
Practically, brute force algorithms are too slow to be useful for real-world problems. However, they are still useful as baselines when benchmarking more advanced algorithms.
Analysis of brute force algorithms with respect to time complexity requires considering the size of the search space often involves performing a combinatorial analysis of the problem. The search space is the set of all possible solutions to a problem.
The table below summarizes the formulas for the size of the search space for different types of problems:
Name |
Ordered? |
Repetition? |
Formula |
Example |
|---|---|---|---|---|
Permutations, with repetition |
Yes |
Yes |
\(n^k\) |
Passwords |
Permutations, without repetition |
Yes |
No |
\(\frac{n!}{(n-k)!}\) |
Sorting |
Combinations, with repetition |
No |
Yes |
\(\frac{(n + k - 1) !}{k! (n-1)!} \) |
Ice-cream sundae |
Combinations, without repetition |
No |
No |
\(\frac{n!}{k!(n-k)!}\) |
Subsets |
where \(n\) is the number of items to choose from and \(k\) is the number of items to choose. Permutations are denoted by \(^{n}P_{r}\) or \(P(n, r)\) and combinations are denoted by \(^{n}C_{r}\) or \(C(n, r)\).
A big reason for why it is strongly recommended to use passwords of length 8 or more, containing a mix of uppercase and lowercase letters, numbers, and special characters is to protect against brute force attacks.
Brute force attacks are a type of attack where the attacker tries to guess a password by trying every possible password.
The table below shows how long it would take to try passwords of different lengths and character sets using brute force attack in 2023:
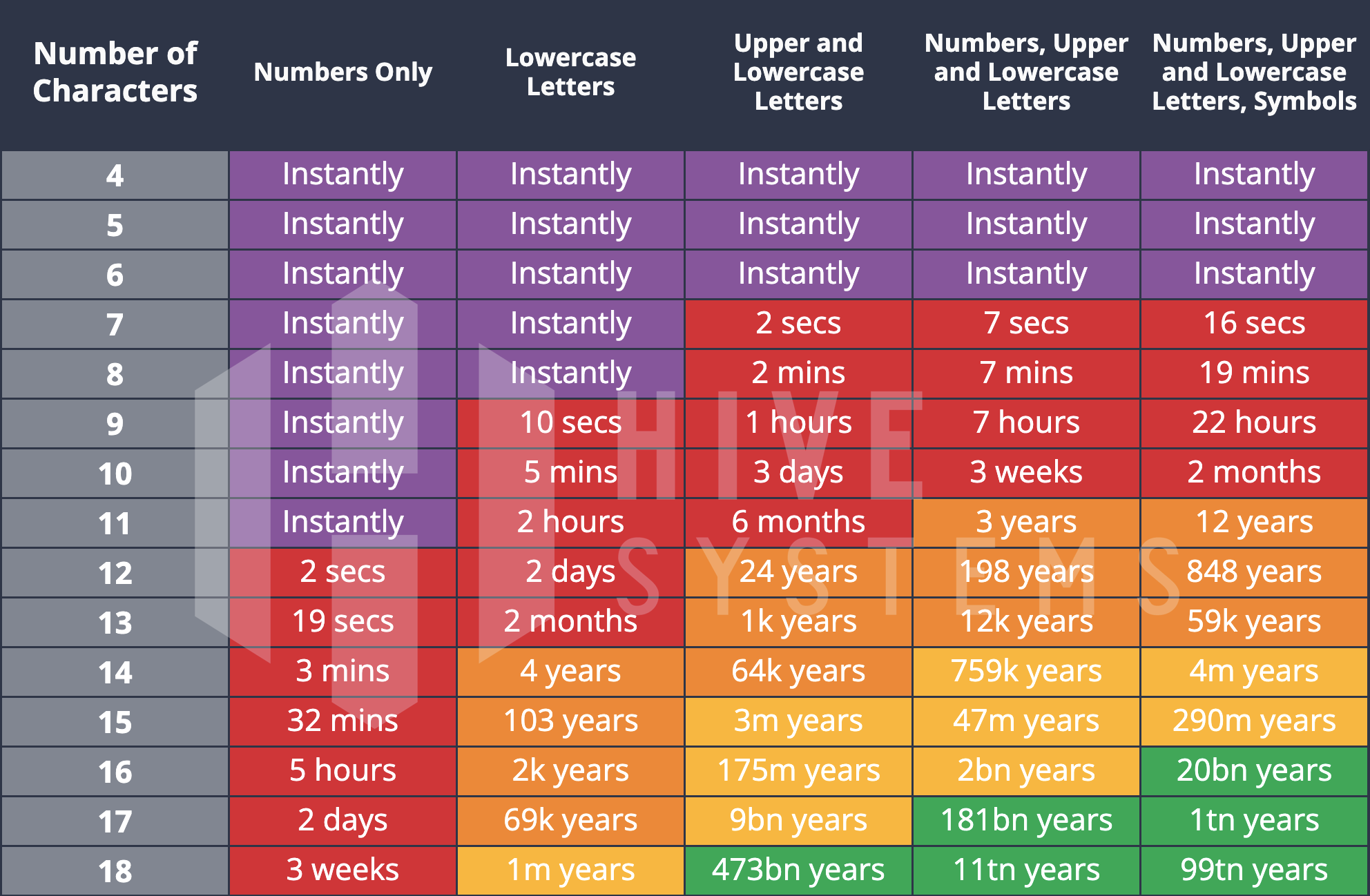
Fig. 2.1 Time taken to exhaustively search through every possible password \(n^k\) of length \(k\) (column 1) and different possible characters \(n\) (columns 2 - 6) using brute force attack in 2023.#
Brute force attacks are very slow because the number of possible passwords increases exponentially with the length of the password.
While here we will focus on using brute force algorithms to solve search and sort problems, virtually any algorithmic problem can be tackled using a brute force approach.
