5.4. Linear Recursion#
Linear recursion is a type of recursion where a function makes a single recursive call.
There are two types of linear recursion:
Head recursion
Tail recursion
In head recursion, the recursive call is the first statement in the function. In tail recursion, the recursive call is the last statement in the function.
Here we will discuss the difference between head and tail recursion and how to convert head recursion to tail recursion. But before that let’s discuss the basic structure of linear recursion.
5.4.1. Basic Structure of Linear Recursion#
The basic structure of a linear recursive function includes the following:
Base case: The base case is the condition that stops the recursion. It is the simplest case of the problem that can be solved directly without recursion. This is generally an
ifstatement that checks if the input is small enough to solve directly. The base case is also often the first statement in the function.Recursive case: The recursive case is the condition that makes the recursive call. It is the condition that reduces the problem to a smaller subproblem. This is generally an
elsestatement that makes the recursive call.Before the recursive call: The statements before the recursive call are performed before the base case is reached. These statements are generally the same for all the recursive calls and often involve passing result of some operation down the recursion.
After the recursive call: The statements after the recursive call are the operations that need to be performed after the recursive call. These operations are generally the same for all the recursive calls.
def f(n):
if n == 0:
print("Base Case, n =", n)
else:
print("Descending towards base case, n =", n)
f(n-1) # recursive call
print("Ascending away from base case, n =", n)
f(5)
Descending towards base case, n = 5
Descending towards base case, n = 4
Descending towards base case, n = 3
Descending towards base case, n = 2
Descending towards base case, n = 1
Base Case, n = 0
Ascending away from base case, n = 1
Ascending away from base case, n = 2
Ascending away from base case, n = 3
Ascending away from base case, n = 4
Ascending away from base case, n = 5
5.4.2. Head Recursion#
In head recursion, the recursive call is the first statement in the function. This means that most of the work is done after the recursive call i.e. while ascending back up away from the base case.
Here is an example of head recursion:
def head_recursion(n):
if n == 0:
#Base case
print("Blastoff! 🚀")
else:
# Recursive case of Head recursion :
# recursive call before anything else
head_recursion(n-1)
print(n)
head_recursion(3)
Blastoff! 🚀
1
2
3
In this example, the function head_recursion does some work before making the recursive call. The recursive call is made with the same arguments as the original call.
Trace of the function head_recursion(3):
head_recursion(3)
head_recursion(2)
head_recursion(1)
head_recursion(0)
print(1)
print(2)
print(3)

Fig. 5.4 Comparison of Head vs. Tail Recursion. The rectangles represent recursive function calls, and circles represent other operations.#
5.4.3. Tail Recursion#
In tail recursion, the recursive call is the last statement in the function. This means that most of the work is done before the recursive call i.e. before reaching the base case, while descending down towards in the recursion.
Here is an example of tail recursion:
def tail_recursion(n):
if n == 0:
# Base case
print("Boomerang 🪃")
else:
# Recursive case of Tail recursion :
# recursive call is the last thing that happens
print(n)
tail_recursion(n-1)
tail_recursion(3)
3
2
1
Boomerang 🪃
In this example, the function tail_recursion makes the recursive call with the modified arguments. The recursive call is the last statement in the function.
Trace of the function tail_recursion(3):
tail_recursion(3)
print(3)
tail_recursion(2)
print(2)
tail_recursion(1)
print(1)
tail_recursion(0)
5.4.4. Recursion vs. Iteration#
Recursion, in particular head or tail recursion, can be thought of as an alternative to iteration.
Any iterative algorithm can be converted to a recursive algorithm and vice versa.
For example, consider the following iterative function to add all numbers in a given list:
def sum_iterative(data):
result = 0
i = 0
while i < len(data):
result = result + data[i]
i = i + 1
return result
The recursive version of the above function is:
def sum_recursive(data):
if data == []:
# base case
return 0
else:
# recursive case
first_element = data[0]
rest_of_list = data[1:]
sum_of_rest = sum_recursive(rest_of_list) # recursive call
result = first_element + sum_of_rest
return result
Let’s see if the two functions produce the same result for the same input:
assert sum_iterative([1, 2, 3, 4]) == sum_recursive([1, 2, 3, 4]), "Test case 1 failed"
assert sum_iterative([99, 100]) == sum_recursive([99, 100]), "Test case 2 failed"
assert sum_iterative([-1, -2, -3]) == sum_recursive([-1, -2, -3]), "Test case 3 failed"
assert sum_iterative([10]) == sum_recursive([10]), "Test case 4 failed"
assert sum_iterative([5, 5, 5]) == sum_recursive([5, 5, 5]), "Test case 5 failed"
print("All test cases passed!")
All test cases passed!
The function sum_iterative and sum_recursive produce the same result for the same input. The iterative function uses a loop to iterate through the list and add the numbers. The recursive function uses the head recursion to add the numbers.
5.4.5. Converting Head Recursion to Tail Recursion#
Head recursion can be converted to tail recursion by using an accumulator. The accumulator is a variable that stores the intermediate result. The accumulator is passed to each recursive call, and the recursive call is the last statement in the function.
Here is the example of summing all numbers in a list using tail recursion:
def sum_tail_recursive(data, current_sum=0):
if data == []:
# base case
return current_sum
else:
# recursive case
first_element = data[0]
rest_of_list = data[1:]
new_sum = current_sum + first_element
result = sum_tail_recursive(rest_of_list, new_sum) # recursive call
return result
Note that the function above uses the optional argument current_sum to store the intermediate result. Optional arguments in python functions are arguments that you are not required to pass when calling the function. If you do not pass the optional argument, the default value is used. In this case, the default value of current_sum is 0. This means when you call the function sum_tail_recursive with just one input say [1, 2, 3], the function will effectively be called as sum_tail_recursive([1, 2, 3], 0). In other words, the value of current_sum will be 0 in the first call. The value of current_sum will be updated in each recursive call and passed to the next recursive call.
As an alternative to using an optional argument, you can define a helper function that takes an additional argument to store the intermediate result, when implementing a tail recursive function. The helper function takes an additional argument (the accumulator) and makes the recursive call. The main function simply calls the helper function with the initial value of the accumulator.
A version of the sum_tail_recursive function, with a helper function, that does not use an optional argument is shown below:
def sum_tail_recursive(data):
return sum_tail_recursive_helper(data, 0)
def sum_tail_recursive_helper(data, current_sum):
if data == []:
# base case
return current_sum
else:
# recursive case
first_element = data[0]
rest_of_list = data[1:]
new_sum = current_sum + first_element
return sum_tail_recursive_helper(rest_of_list, new_sum) # recursive call
5.4.6. Avoiding Linear Recursion#
Linear recursion is considered a bad practice in Python, since the Python compiler does not handle optimization for tail recursive calls. The recursive solution in cases like this use more system resources than the equivalent iterative solution.
In Python, it is better to use an iterative solution instead of a recursive solution. The iterative solution is more efficient and easier to understand, in most cases.
5.4.7. Positive Example: Factorials#
Every recursive function we have seen so far is better implemented iteratively.
However, there are some functions that are more naturally expressed recursively. The canonical example is the factorial function.
Let’s consider the factorial function, defined by
Note that the factorial function is naturally expressed recursively. Note how the function definition includes the recursive case as well as the base case.
This means that the recursive implementation is more natural and easier to understand than the iterative implementation.
def factorial(n):
if n == 1:
return 1
else:
return n * factorial(n-1)
We can watch this function in action computing 6!, as shown in figure below:
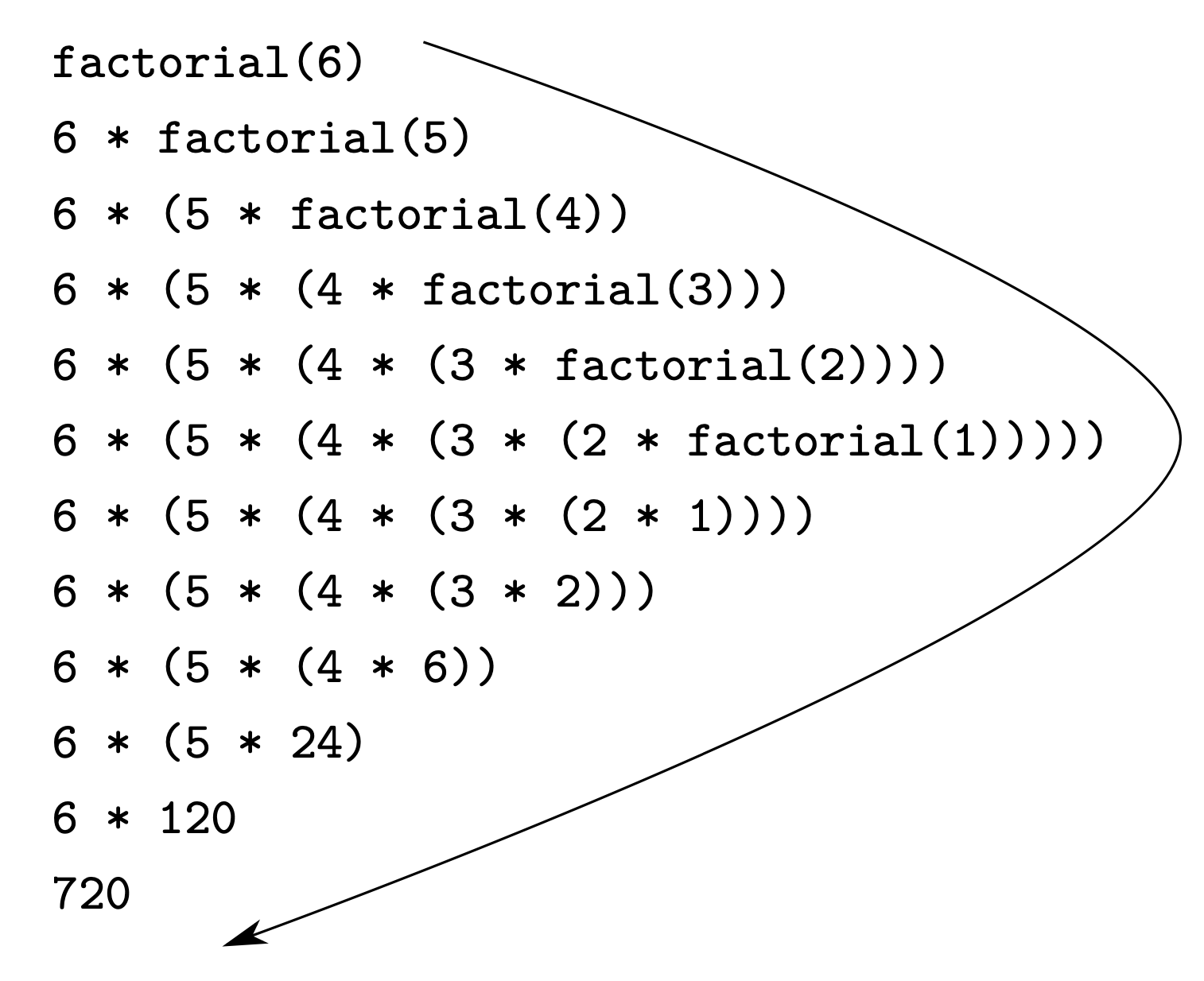
Fig. 5.5 A linear recursive process for computing 6!#
The iterative implementation of the factorial function requires taking a different perspective on computing factorials. We could describe a rule for computing n! by specifying that we first multiply 1 by 2, then multiply the result by 3, then by 4, and so on until we reach n. More formally, we maintain a running product, together with a counter that counts from 1 up to n. We can describe the computation by saying that the counter and the product simultaneously change from one step to the next according to the rule
and stipulating that \(n!\) is the value of the product when the counter exceeds \(n\).
def factorial_iterative(n):
result = 1
for i in range(1, n+1):
result = result * i
return result
While the iterative implementation is equally correct, it is less natural and does not align with the mathematical definition of the mathematical function.
