7.2. Queues#
A queue is a collection of items that are maintained in a sequence and can be modified by the addition or removal of items at opposite ends.
An example of a queue is a line of customers waiting for service of some kind. In most cases, the first customer in line is the next customer to be served. There are exceptions, though. At airports, customers whose flights are leaving soon are sometimes taken from the middle of the queue. At supermarkets, a polite customer might let someone with only a few items go first.

Queues are used in a variety of applications, including simulations, task scheduling, and managing data in a network. The end where items are added is called the rear, and the end where items are removed is called the front.
The queue is sometimes called a FIFO (first-in-first-out) list because the first item added is the first item that can be removed. This is analogous to a line of customers waiting for service. The first customer in line is the first customer to be served.

The rule that determines who goes next is called the queueing policy. The simplest queueing policy is called FIFO, for first- in-first-out. The most general queueing policy is priority queueing, in which each customer is assigned a priority and the customer with the highest priority goes first, regardless of the order of arrival. We say this is the most general policy because the priority can be based on anything: what time a flight leaves; how many groceries the customer has; or how important the customer is. Of course, not all queueing policies are fair, but fairness is in the eye of the beholder.
7.2.1. Operations#
The Queue ADT is defined by the following operations:
Enqueue: Adds a new item to the back of the queue. It needs the item and returns nothing.

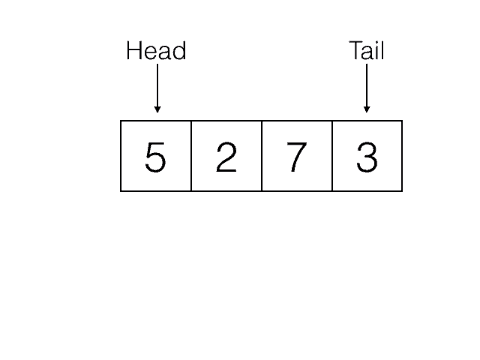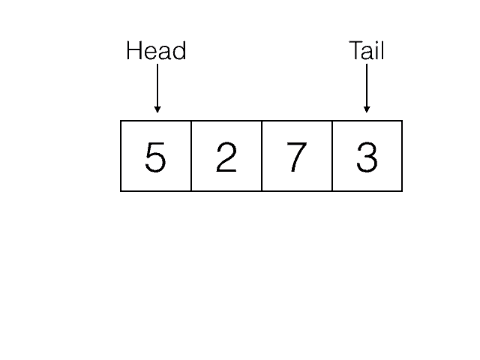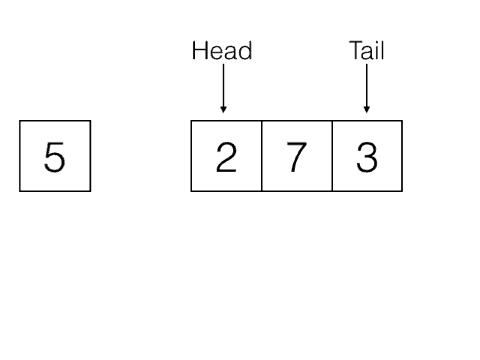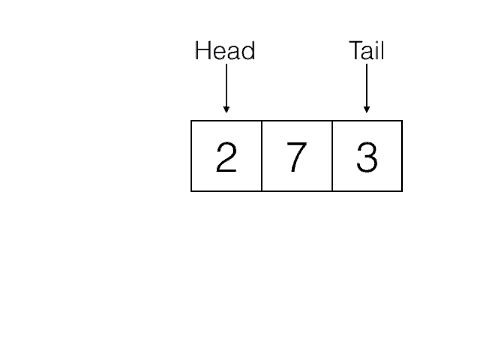
Dequeue: Removes the item from the queue that was least recently added. It needs no parameters and returns the item. The queue is modified.
Is_Empty: Tests to see whether the queue is empty. It needs no parameters and returns a boolean value.
Size: Returns the number of items in the queue. It needs no parameters and returns an integer.
Front: Returns the item least recently added to the queue. It needs no parameters and returns the item. The queue is not modified.
Equally important to the operations that a queue supports is the operations that it does not support.
Queues do not support:
Random Access: You cannot access an arbitrary element in the queue. You can only access the element at the front of the queue.
❌ Read elements at arbitrary positions.
✅ You can only access the element at the front or the back of the queue using thefrontandbackoperations.
❌ Insert elements at arbitrary positions.
✅ You can only insert elements at the back of the queue using theenqueueoperation.
❌ Remove elements from arbitrary positions.
✅ You can only remove elements from the front of the queue using thedequeueoperation.
Whether you are adding, removing, or accessing elements, you can only interact with the front or the back of the queue. This is what makes queues different from other data structures like lists or arrays.
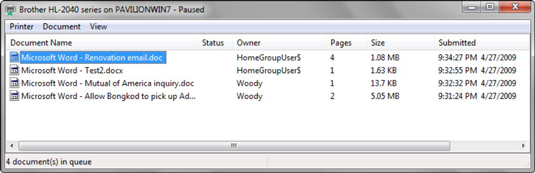
7.2.2. Application 1: Printer Queue#
Imagine you are working in a computer lab and you have to print a document. You send the document to the printer, but there are already other documents in the printer queue. The printer will print the documents in the order they were sent. This is a perfect example of a queue. The first document sent to the printer will be the first one printed.
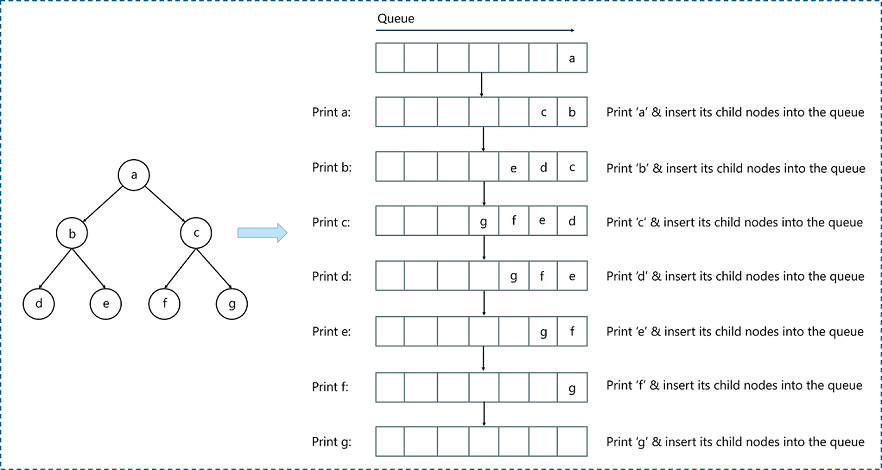
7.2.3. Application 2: Breadth-First Search#
Queues are used in algorithms like Breadth-First Search (BFS). BFS is an algorithm used to traverse or search tree or graph data structures. It starts at the tree root (or some arbitrary node of a graph) and explores all of the neighbor nodes at the present depth prior to moving on to the nodes at the next depth level.
7.2.4. Application 3: Task Scheduling#
Queues are used in task scheduling algorithms. For example, in an operating system, the CPU scheduler uses a queue to manage the tasks that are waiting to be executed. The tasks are executed in the order they were added to the queue.

7.2.5. Implementation#
There are several ways to implement a queue. The most common way is to use a list. In Python, you can use a list to implement a queue. You can use the append() method to add elements to the back of the queue and the pop() method to remove elements from the front of the queue.
class Queue:
def __init__(self):
self.__data = []
def enqueue(self, item):
self.__data.append(item)
def dequeue(self):
return self.__data.pop(0)
def is_empty(self):
return len(self.__data) == 0
def size(self):
return len(self.__data)
def __str__(self):
return str(self.__data)
q = Queue()
q.enqueue(1)
q.enqueue(2)
q.enqueue(3)
assert q.size() == 3, 'Test 1 Failed'
assert q.dequeue() == 1, 'Test 2 Failed'
assert q.dequeue() == 2, 'Test 3 Failed'
assert q.size() == 1, 'Test 4 Failed'
assert q.is_empty() == False, 'Test 5 Failed'
assert q.dequeue() == 3, 'Test 6 Failed'
print('All tests passed')
All tests passed
7.2.6. Space and Time Complexity#
The space complexity of a queue is O(n), where n is the number of elements in the queue. This is because we are using a list to store the elements of the queue.
The time complexity of the enqueue and dequeue operations is O(1). This is because we are using the append() and pop(0) methods of the list to add and remove elements from the queue. These methods have a time complexity of O(1).
The time complexity of the is_empty and size operations is also O(1). This is because we are just checking the length of the list, which has a time complexity of O(1).
The time complexity of the front operation is O(1). This is because we are just returning the first element of the list, which has a time complexity of O(1).
