Trees

Trees

Trees are a fundamental data structure in computer science. They are hierarchical data structures that consist of nodes, where each node contains a data value and references to its children nodes. Trees are used to represent hierarchical relationships between data elements, such as file systems, organization charts, and abstract syntax trees.

Types of Trees

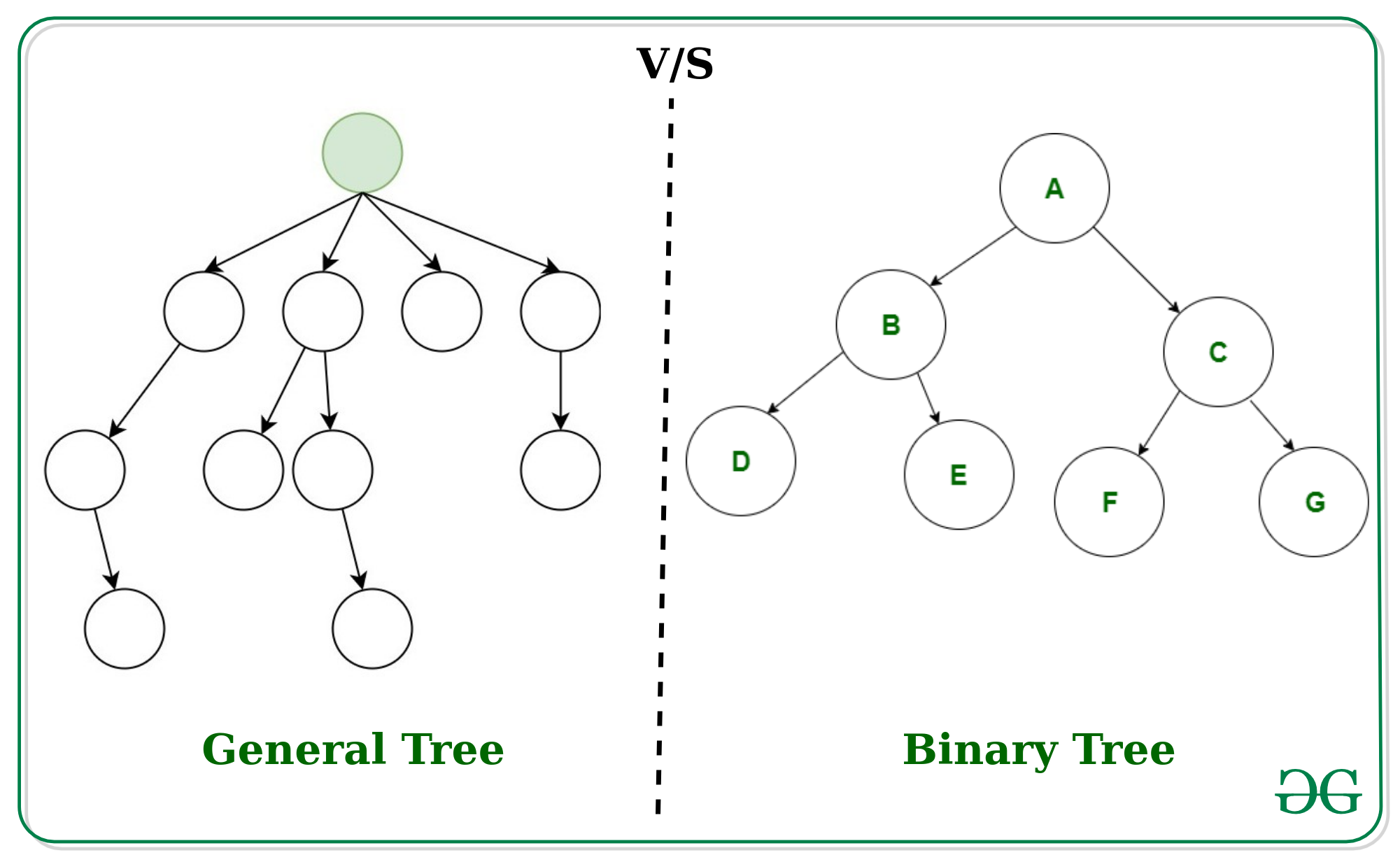
Binary Tree: A tree in which each node has at most two children nodes.

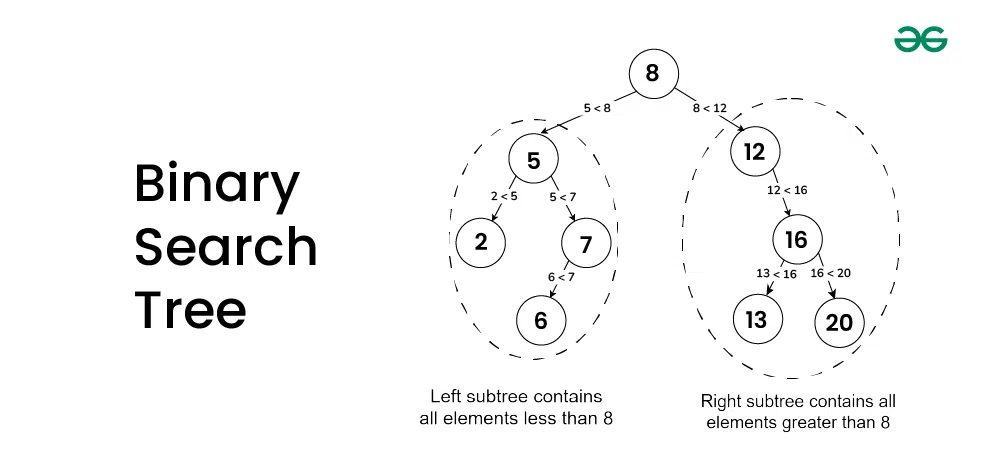
Binary Search Tree (BST): A binary tree in which the left subtree of a node contains only nodes with values less than the node’s value, and the right subtree contains only nodes with values greater than the node’s value.

Full Binary Tree: A binary tree in which every node has either zero or two children.
Complete Binary Tree: A binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
Degenerate Tree: A tree in which each parent node has only one child node.
Perfect Binary Tree: A binary tree in which all interior nodes have two children and all leaves have the same depth or same level.
Balanced Binary Tree: A binary tree in which the heights of the two subtrees of every node differ by at most one.

Properties of Trees

Trees have the following properties:

A tree with n nodes has n-1 edges.
A tree with height h has at most 2^h - 1 nodes.
A binary tree with height h has at most 2^(h+1) - 1 nodes.
The height of a binary tree with n nodes is log(n+1) - 1.
The height of a binary search tree with n nodes is log(n).
The time complexity of operations on a binary search tree is O(log(n)) on average and O(n) in the worst case.

Operations on Trees

Search: Finding a specific node in the tree.

Depth First Search (DFS)

A traversal algorithm that explores as far as possible along each branch before backtracking.

def dfs(root, target):
	if root is None:
		return False
	if root.val == target:
		return True
	return dfs(root.left, target) or dfs(root.right, target)

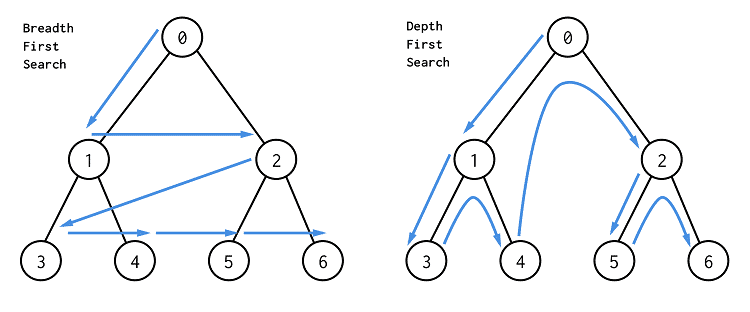
Breadth First Search (BFS)

A traversal algorithm that explores all the nodes at the present depth before moving on to the nodes at the next depth.

def bfs(root, target):
	if root is None:
		return False
	queue = [root]
	while queue:
		node = queue.pop(0)
		if node.val == target:
			return True
		if node.left:
			queue.append(node.left)
		if node.right:
			queue.append(node.right)
	return False

Traversal

Traversal is the process of visiting each node in the tree in a specific order.

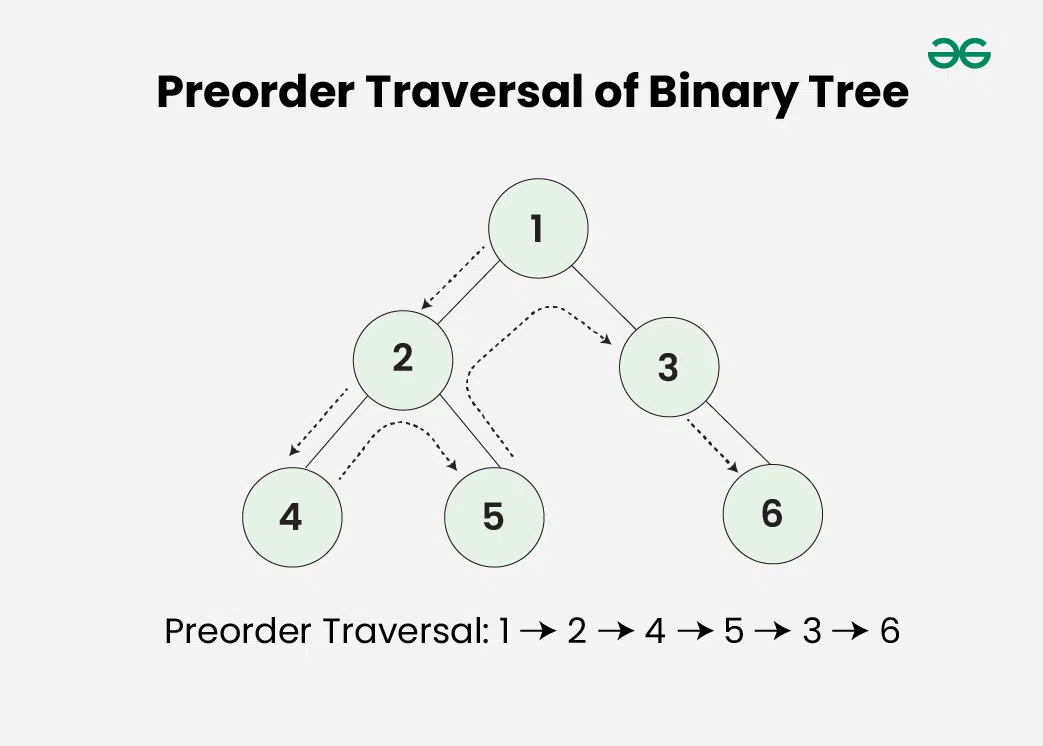
Preorder Traversal (DFS: Root-Left-Right)

Visit the root node first, then recursively do a preorder traversal of the left subtree, followed by a preorder traversal of the right subtree.

def preorder_traversal(root):
	if root is None:
		return
	print(root.val) 		# Visit the root node
	preorder_traversal(root.left) 	# Visit the left subtree
	preorder_traversal(root.right) 	# Visit the right subtree

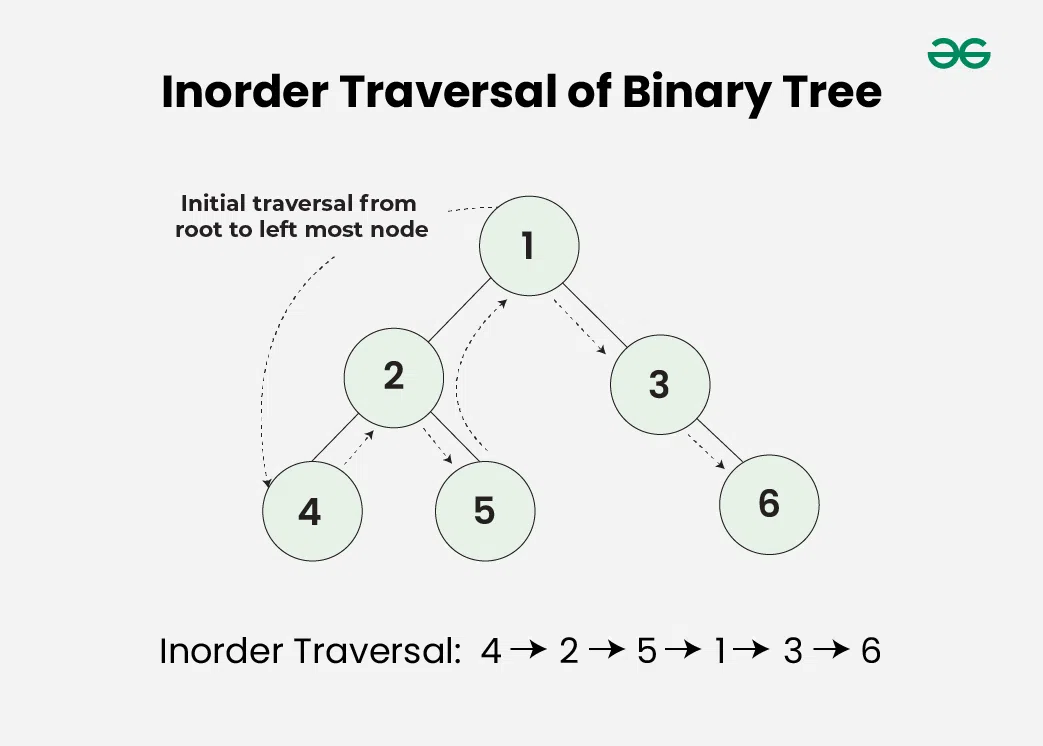
In-order Traversal (DFS: Left-Root-Right)

Visit the left subtree first, then visit the root node, followed by a recursive inorder traversal of the right subtree.

def inorder_traversal(root):
	if root is None:
		return
	inorder_traversal(root.left) 	# Visit the left subtree
	print(root.val) 		# Visit the root node
	inorder_traversal(root.right) 	# Visit the right subtree

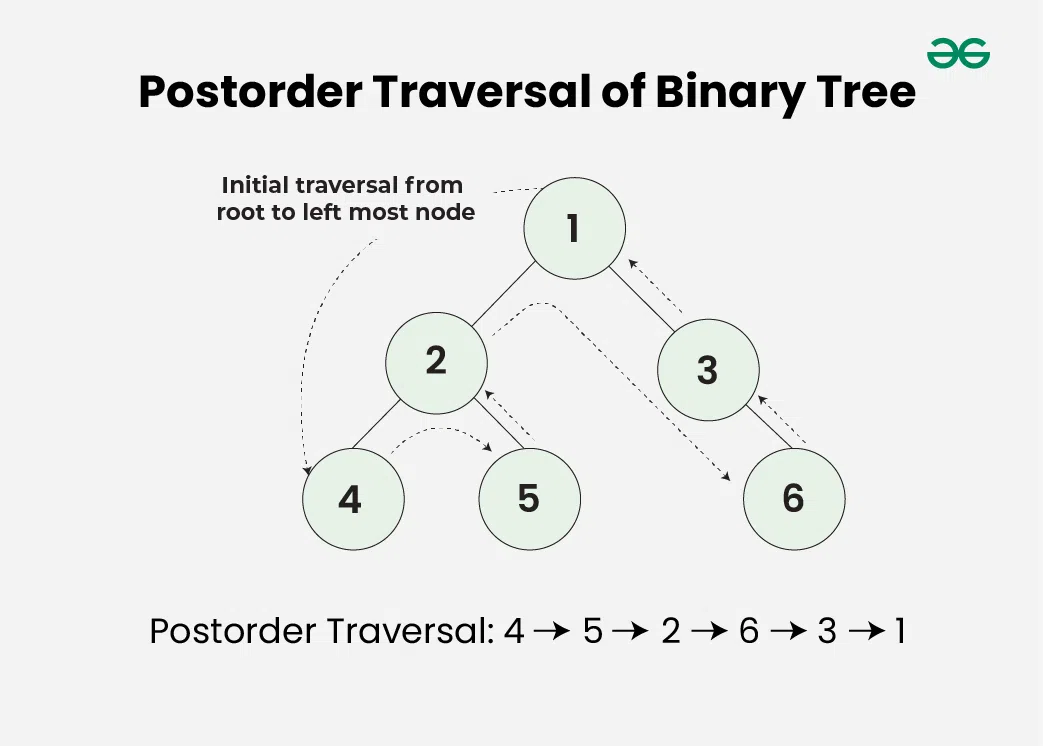
Post-order Traversal (DFS: Left-Right-Root)

Recursively do a postorder traversal of the left subtree, followed by a postorder traversal of the right subtree, and then visit the root node.

def postorder_traversal(root):
	if root is None:
		return

	postorder_traversal(root.left) # Visit the left subtree
	postorder_traversal(root.right) # Visit the right subtree
	print(root.val) # Visit the root node

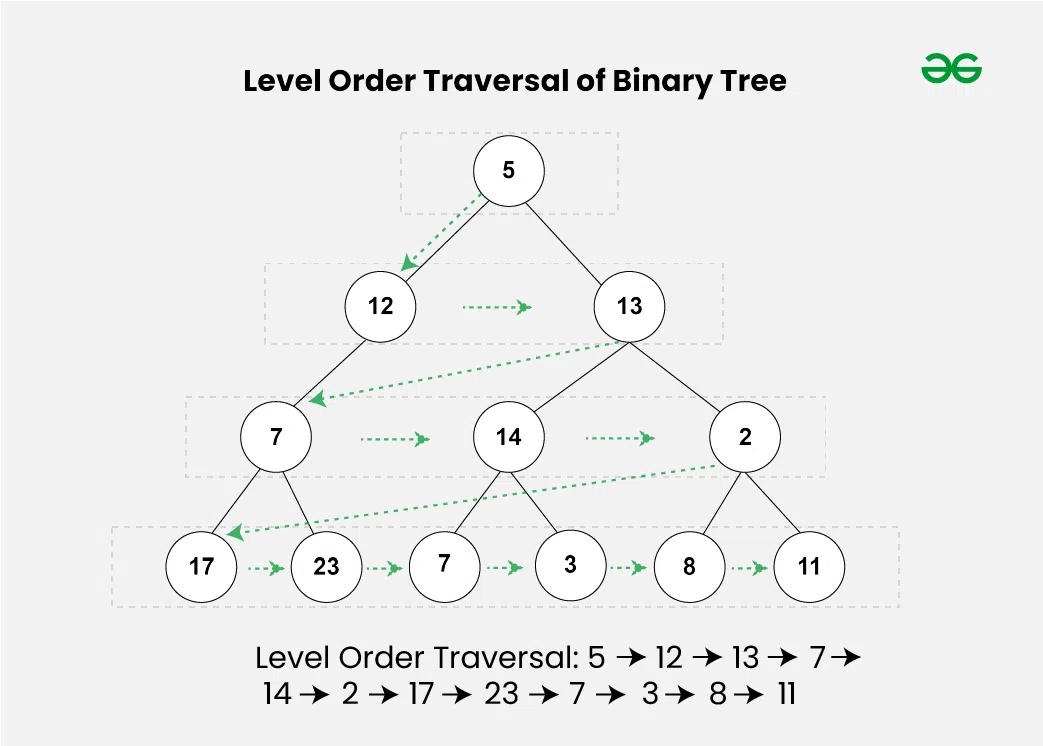
Level-order Traversal (BFS)

Level-order traversal is a breadth-first search (BFS) algorithm that visits all the nodes at the present depth before moving on to the nodes at the next depth.

def level_order_traversal(root):
	if root is None:
		return
	queue = [root]
	while queue:
		node = queue.pop(0)
		print(node.val)
		if node.left:
			queue.append(node.left)
		if node.right:
			queue.append(node.right)

Binary Search Tree Operations

Insertion

Adding a new node to the tree.

class TreeNode:
	def __init__(self, val=0, left=None, right=None):
		self.val = val
		self.left = left
		self.right = right


def insert(root, val): 
	"""
	Inserts a new node with value `val` into the binary search tree.
	"""
	if root is None:
		return TreeNode(val)
	if val < root.val:
		root.left = insert(root.left, val)
	else:
		root.right = insert(root.right, val)
	return root

Deletion

Removing a node from the tree.

def delete(root, val):
	"""
	Deletes a node with value `val` from the binary search tree.
	"""
	if root is None:
		return root
	if val < root.val:
		root.left = delete(root.left, val)
	elif val > root.val:
		root.right = delete(root.right, val)
	else:
		if root.left is None:
			return root.right
		elif root.right is None:
			return root.left
		root.val = find_min(root.right)
		root.right = delete(root.right, root.val)
	return root

Update

Changing the data value of a node in the tree.

def update(root, target, new_val):
	"""
	Updates the value of the node with value `target` to `new_val`.
	"""
	if root is None:
		return
	if root.val == target:
		root.val = new_val
	update(root.left, target, new_val)
	update(root.right, target, new_val)