Backtracking
Problems
Question 1. Combination Sum
Medium
Solution
Given an array of distinct integers candidates and a target integer target, return a list of all unique combinations of candidates where the chosen numbers sum to target. You may return the combinations in any order.
The same number may be chosen from candidates an unlimited number of times. Two combinations are unique if the frequency of at least one of the chosen numbers is different.
It is guaranteed that the number of unique combinations that sum up to target is less than 150 combinations for the given input.
Example
Input: candidates = [2,3,6,7], target = 7 Output: [[2,2,3],[7]]
Explanation: 2 and 3 are chosen, the sum is 5 and 2 is chosen again to make the sum 7. No other combinations are possible.
def combination_sum(candidates, target):
pass
assert combination_sum([2,3,6,7], 7) == [[2,2,3],[7]], "Test case 1 failed"
assert combination_sum([2,3,5], 8) == [[2,2,2,2],[2,3,3],[3,5]], "Test case 2 failed"
assert combination_sum([2], 1) == [], "Test case 3 failed"
print("Test cases passed :)")
Question 2. Word Search
Medium
Solution
Given an m x n grid of characters board and a string word, return true if word exists in the grid.
The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.
Example
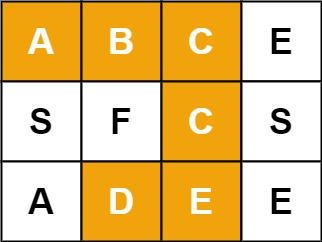
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED" Output: true
def exist(board, word):
pass
assert exist([
["A","B","C","E"],
["S","F","C","S"],
["A","D","E","E"]
], "ABCCED") == True, "Test case 1 failed"
assert exist([
["A","B","C","E"],
["S","F","C","S"],
["A","D","E","E"]
], "SEE") == True, "Test case 2 failed"
assert exist([
["A","B","C","E"],
["S","F","C","S"],
["A","D","E","E"]
], "ABCB") == False, "Test case 3 failed"
print("Test cases passed :)")