Brute Force

Brute Force

Brute Force Algorithms are exactly what they sound like – straightforward methods that relying on sheer computing power to try every possibility rather than using insight to efficiently narrow down the possibilities. Brute force algorithms are also known as “exhaustive search” algorithms, because they try all possible answers until they find the right one.

For example, imagine you have a small padlock with 4 digits, each from 0-9. You forgot your combination, but you don’t want to buy another padlock. Since you can’t remember any of the digits, you have to use a brute force method to open the lock. So you set all the numbers back to 0 and try them one by one: 0001, 0002, 0003, and so on until it opens. In the worst case scenario, it will take you 10,000 tries to open the lock.

Practically, brute force algorithms are too slow to be useful for real-world problems. However, they are still useful as baselines when benchmarking more advanced algorithms.

Analysis of brute force algorithms with respect to time complexity requires considering the size of the search space often involves performing a combinatorial analysis of the problem. The search space is the set of all possible solutions to a problem.

The table below summarizes the formulas for the size of the search space for different types of problems:

Name	Ordered?	Repetition?	Formula	Example
Permutations, with repetition	Yes	Yes	$n^k$	Passwords
Permutations, without repetition	Yes	No	$\frac{n!}{(n-k)!}$	Sorting
Combinations, with repetition	No	Yes	$\frac{(n + k - 1) !}{k! (n-1)!} $	Ice-cream sundae
Combinations, without repetition	No	No	$\frac{n!}{k!(n-k)!}$	Subsets

where n is the number of items to choose from and $k$ is the number of items to choose. Permutations are denoted by ^{n}P_{r} or $P(n, r)$ and combinations are denoted by $^{n}C_{r}$ or $C(n, r)$.

A big reason for why it is strongly recommended to use passwords of length 8 or more, containing a mix of uppercase and lowercase letters, numbers, and special characters is to protect against brute force attacks.

Brute force attacks are a type of attack where the attacker tries to guess a password by trying every possible password.

\[\text{Number of possible passwords} = \text{Number of possible characters}^{~\text{Length of password}}\] \[\text{Number of possible passwords of length 8, containing only lowercase english letters} = 26^8 = 208,827,064,576\]

The table below shows how long it would take to try passwords of different lengths and character sets using brute force attack in 2023:

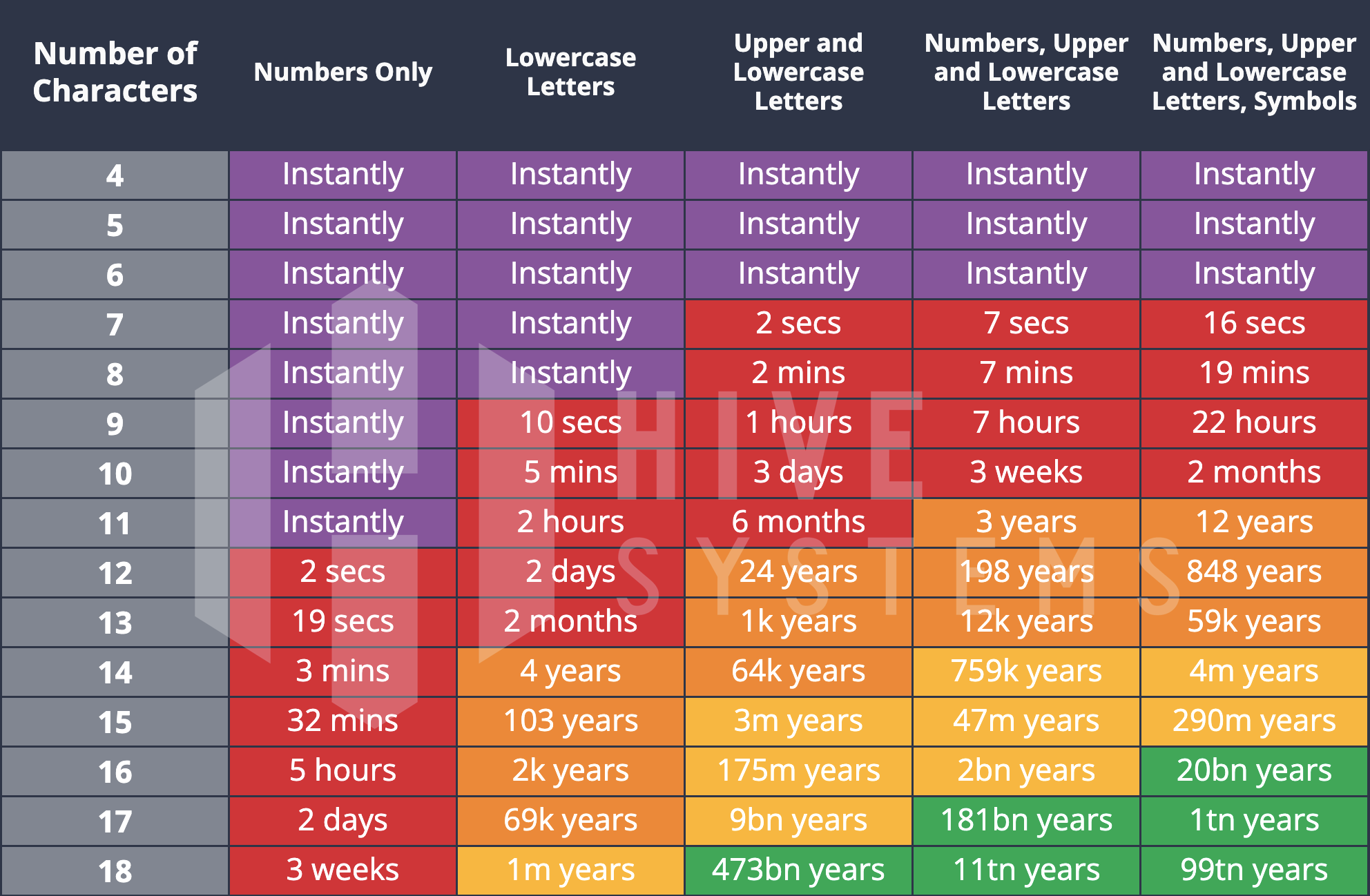
Brute force attacks are very slow because the number of possible passwords increases exponentially with the length of the password.

While here we will focus on using brute force algorithms to solve search and sort problems, virtually any algorithmic problem can be tackled using a brute force approach.

Linear Search

Linear Search (also known as Sequential Search) is a brute force search algorithm that finds a target value within a list by sequentially checking each element of the list until a match is found.

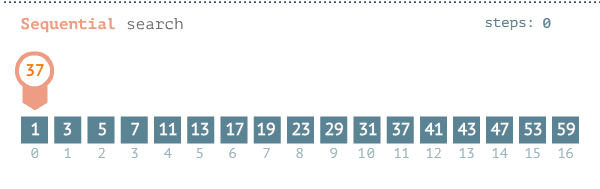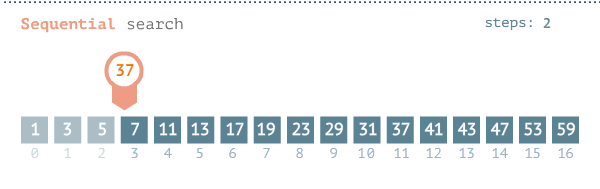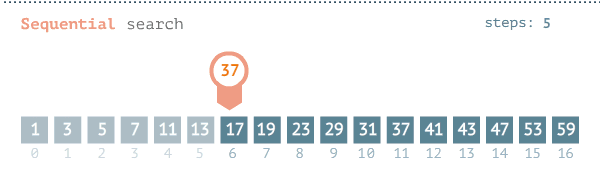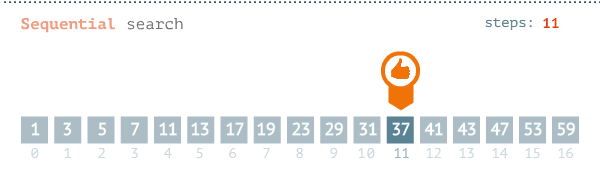
The pseudocode for the algorithm is as follows:

Python implementation of the algorithm is as follows:

data = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
query = 5

def linear_search(data, query):
    """
    Returns the index position of the target if found, else returns -1
    """
    i = 0
    while i < len(data):
        if data[i] == query:
            return i
    return -1

linear_search(data, query)

The time complexity of the above algorithm is O(n) since in the worst case we have to iterate over the entire list to find the target.

In best case, the target is found at the first index, thus the best case is O(1).

Assuming uniform distribution of the target value, the average case is If each element is equally likely to be searched, then linear search has an average case of $ \frac{n+1}{2}$ comparisons. Thus, the average case is O(n).

The space complexity of the above algorithm is O(1) since we are not using any extra space.

Bogosort

Bogosort (also known as Permutation sort or Stupid sort) is the brute-force approach to sorting.

It enumerates all permutations of the input until it finds the sorted version.

The name comes from the word “bogus” because it is a bogus sorting algorithm.

There are many variants of bogosort. The difference between the two most common variants is that of determinism and randomness. The deterministic version enumerates all permutations until it encounters a sorted one whereas the randomized version permutes its input randomly. Here, we are discussing the deterministic version.

Note that computing all permutations of a given list is in itself a hard algorithmic problem. Here, we are assuming that we have a function that can compute all permutations of a given list.

The following is an implementation of bogosort in Python:

import itertools

def is_sorted(arr):
    for i in range(len(arr) - 1):
        if arr[i] > arr[i + 1]:
            return False
    return True

def bogo_sort(arr):
    all_permutations = itertools.permutations(data)
    for permutation in all_permutations:
        if is_sorted(permutation):
            return permutation
    return None

Note that the above implementation uses the built-in itertools library to compute all permutations of the input list.

The time complexity of the above algorithm is O(n!) since we have to compute all permutations of the input list.

Two Sum Problem

The Two Sum Problem is a classic algorithmic problem that asks the following question: given an array of integers nums and an integer target, return indices of the two numbers such that they add up to target.

The brute force approach to solving the Two Sum Problem is to iterate over the array and for each element, check if there is another element in the array that sums to the target.

The following is an implementation of the Two Sum Problem in Python:

def two_sum(nums, target):
    for i in range(len(nums)):
        for j in range(i + 1, len(nums)):
            if nums[i] + nums[j] == target:
                return [i, j]
    return None

The time complexity of the above algorithm is O(n^2) since we have to iterate over the array twice to find the two numbers that sum to the target.