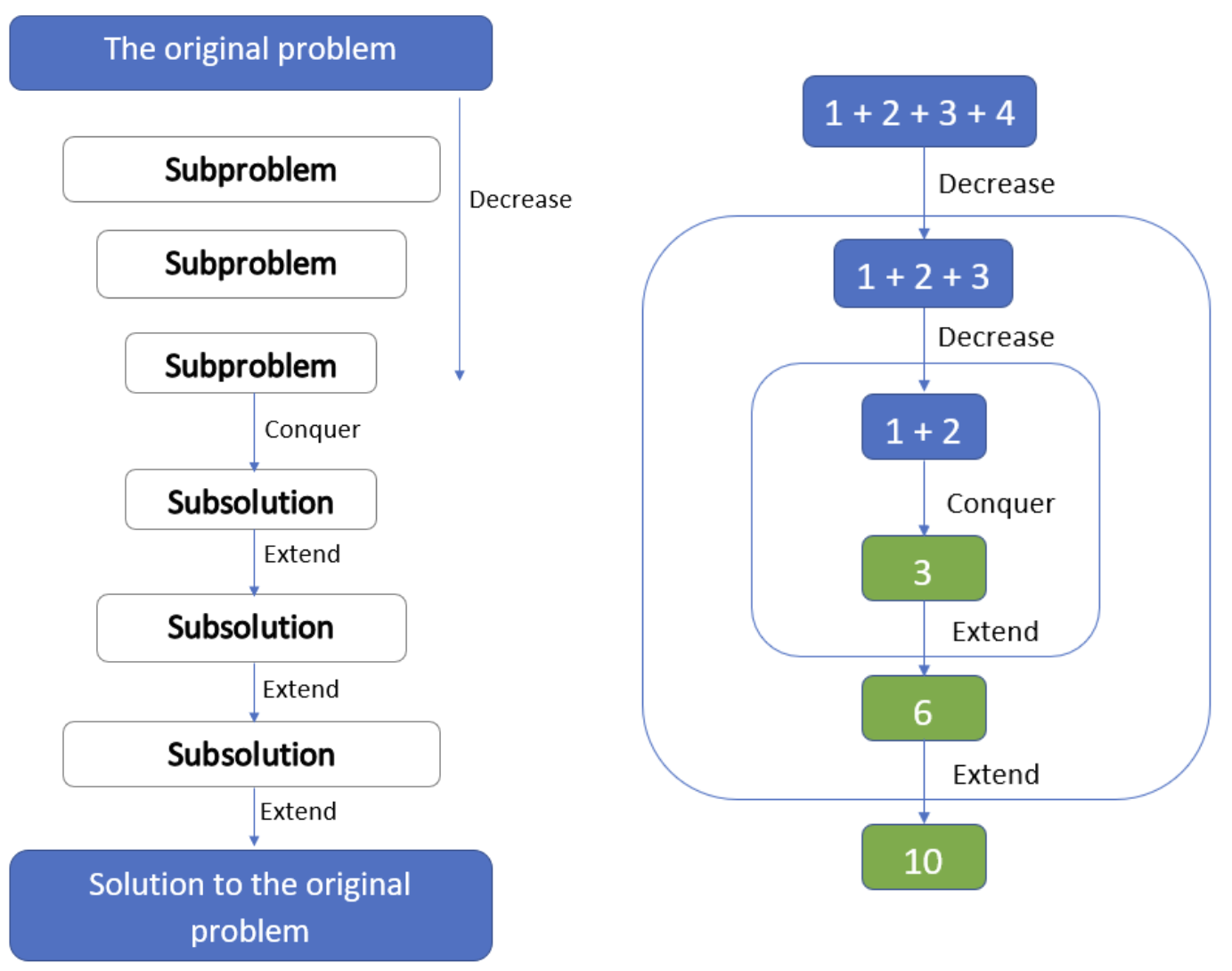
Decrease & Conquer

Decrease & Conquer
Selection Sort
Insertion Sort

Decrease and conquer algorithms take the following approach:

Decrease or reduce the problem instance to smaller instance of the same problem.
Conquer the problem by solving smaller instance of the problem.
Extend solution of smaller instance to obtain solution to original problem .

Basic intuition of the decrease-and-conquer technique is based on exploiting the relationship between a solution to a given instance of a problem and a solution to its smaller instance. This approach is also known as incremental or inductive approach.

Decrease and Conquer algorithms contrasts with the Divide and Conquer approach in the scope of the problem reduction.

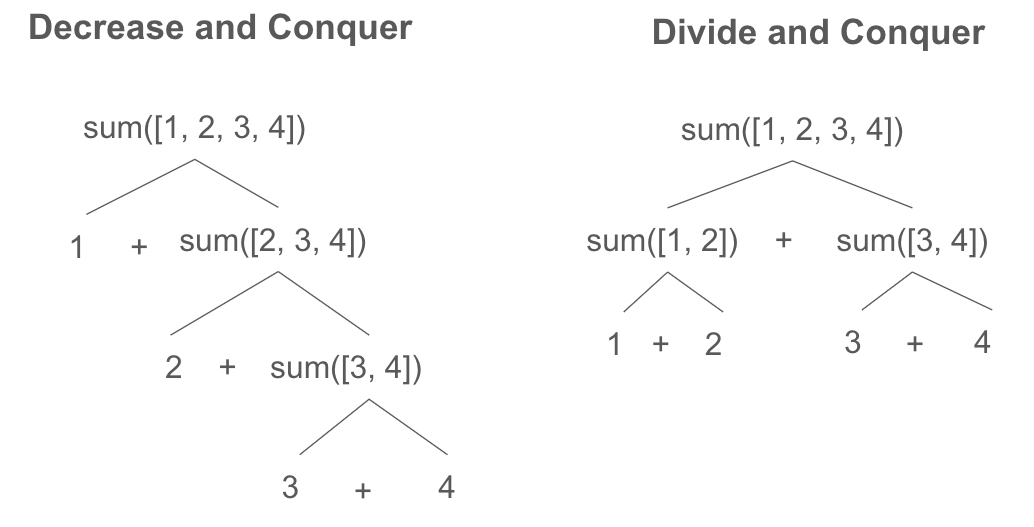
Decrease and Conquer	Divide and Conquer
Problem is reduced to a smaller instances in a chain like manner, piecing off one element at a time	Problem is reduced to two or more smaller instances in a tree like manner
Decrease by a constant amout Think subtraction `n = n - constant` at each step	Decrease by a constant factor Think division `n = n / constant` at each step
Example: Insertion, Selection Sort	Example: Binary Search, Merge Sort

Selection Sort

Selection sort is a simple decrease and conquer sorting algorithm that works by maintaining two sublists in a given array:

The sublist which is already sorted.
Remaining sublist which is unsorted.

The algorithm iteratively “selects” the smallest (for ascending order) element from the unsorted sublist and appends it to the end of the sorted sublist. This process continues until the unsorted sublist is empty.

Note that the algorithm does not require any extra space and is thus an in-place sorting algorithm. The two sublists are maintained by a single variables tracking the first element of the unsorted sublist. Everything before this variable is sorted and everything after it is unsorted.

Selection sort “conquers” the sorting problem by “decreasing” the size of the unsorted sublist by one in each iteration.

Algorithm

The selection sort algorithm, conceptually in broad steps, works as follows:

Initialize a iterator $i$ to $0$.
Identify the smallest element in the unsorted sublist (from $i$ to $n-1$).
Swap the smallest element with the element at index $i$.
Increment $i$ by $1$.
Repeat steps 2-4 until $i$ is equal to $n-1$.

Implementation

def find_min(data):
    min_index = 0
    for i in range(1, len(data)):
        if data[i] < data[min_index]:
            min_index = i
    return min_index

def selection_sort(data):
    n = len(data)
    for i in range(n):
        find_min(data[i:])
        data[i], data[min_index] = data[min_index], data[i]
    return data

Analysis

Time Complexity of selection sort is O(n^2) in all cases.

In the worst case, the list is sorted in reverse order. In this case, the algorithm will perform $n$ comparisons and $n$ swaps. Thus, the time complexity is O(n^2).

In the best case, the list is already sorted. In this case, the algorithm still performs n^2 comparisons but does $0$ swaps. Thus, the time complexity is O(n^2).

In the average case, the list is not sorted. In this case, the algorithm will perform $n$ comparisons and $n/2$ swaps. Thus, the time complexity is $O(n^2)$.

Space Complexity of selection sort is $O(1)$. This is because the algorithm sorts the list in-place.

Insertion Sort

Insertion sort is a sorting algorithm that works the way we sort playing cards in our hands.

The algorithm works by maintaining two sublists in a given array:

The sublist which is already sorted.
Remaining sublist which is unsorted.

The algorithm iteratively “inserts” the next element from the unsorted sublist into the correct position in the sorted sublist. This process continues until the unsorted sublist is empty.

Similar to selection sort, the algorithm does not require any extra space the two sublists are maintained by a single variables tracking the first element of the unsorted sublist. Everything before this variable is sorted and everything after it is unsorted.

Steps

The algorithm works as follows:

Initialize a iterator i to 1.
Call the element at ith location key i.e. key = L[i].
Iterate over sublist to the left of $i$ from right to left i.e. iterate over the list from i-1 to 0 using an iterator called j. The sublist from i-1 to 0 is the sorted sublist.
For all values L[j] > key, shift them one place to the right i.e. set L[j+1] to L[j] until L[j] > key.
Once you find a value L[j] <= key, you’ve found the correct location of key. Set L[j+1] to key.
Increment i by 1 and repeat steps 2-5 until i is equal to n-1.

Implementation

def insertion_sort(data):
    n = len(data)
    for i in range(1, n):
        key = data[i]
        j = i - 1
        while j >= 0 and key < data[j]:
            data[j + 1] = data[j]
            j -= 1
        data[j + 1] = key
    return data

Analysis

The time complexity of insertion sort depends on the initial order of the elements in the input array.

In the worst case, the array is sorted in reverse order. In this case, the algorithm will perform $n$ comparisons and n(n-1)/2 swaps. Thus, the time complexity is O(n^2).

In the average case, the array is randomly ordered. In this case, the algorithm will perform $n$ comparisons and n(n-1)/4 swaps. Thus, the time complexity is O(n^2).

In the best case, the array is already sorted. In this case, the algorithm will perform n comparisons and 0 swaps. Thus, the time complexity is O(n). Note that the best case of insertion sort is better than the best case of selection sort.

The space complexity of insertion sort is O(1) in all cases as the algorithm does not require any extra space.

Comparison with Selection Sort

Selection and Insertion sort are similar algorithms with some subtle but key differences.

Similarities

They are similar in that they are

Both decrease and conquer sorting algorithms
Both maintain two sublists in a given array:
- The sublist which is already sorted.
- Remaining sublist which is unsorted.
Both have a time complexity of O(n^2)
Both are in-place sorting algorithms
The space complexity of both is O(1)

Differences

They two key difference in that:

In selection sort, most of the work done is in “selecting” (finding) the smallest element in the unsorted sublist.

In insertion sort, most of the work is done in “inserting” the next element from the unsorted sublist into the correct position in the sorted sublist.

Depending on the implementation and the data, insertion sort can, in the best case, be faster than selection sort.